nanoteyep

nanoteyep

DataScience trainee

© 2022

Dark Mode

Machine Learning with Graph - 3. Node-level tasks and Features
Jul 7, 2022
  • GNN

Node-level tasks and Features

1. Node-level Features

Node-level task의 목표는 Node의 구조와 위치정보를 Characterize 하는 것 입니다.
이 때 사용되는 Features가 Node-level Features 이며 총 4가지 Features에대해 알아 볼 것 입니다.

  • Node degree
  • Node Centrality
  • Clustring coefficient
  • Graphlets

2. Node degree

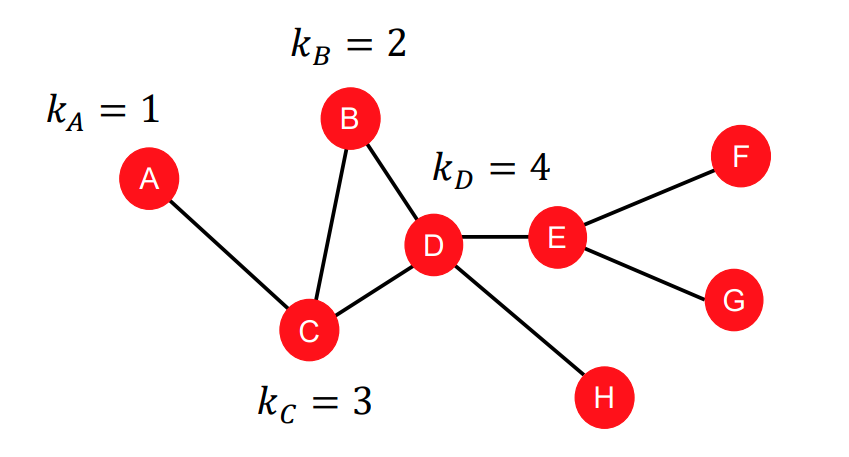
node_1

Node degree는 이웃 Node와 연결된 edge의 갯수 이며 $k_{v}$라고 표현합니다.

3. Node centrality

Node degree가 이웃된 Node의 갯수만을 고려한 Features라면 Node centrality는 그래프 상에서 Node의 중요도를 의미하며 $c_{v}$라고 표현합니다.
중요도를 측정하는 방법은 다양한 방법이 있지만 3가지 소개하려고 합니다.

  • Eigenvector centrality
    Node $v$가 important node $u$에 둘러싸여 있다면 $v$는 imporatnt한 node일 것 입니다.
    그렇기 때문에 $v$의 centrality는 이웃 nodes들의 합이라는 모델을 작성 할 수 있으며 이를 식으로 작성하고 풀기 위해 matrix form으로 재 작성 한 식이 아래와 같습니다.

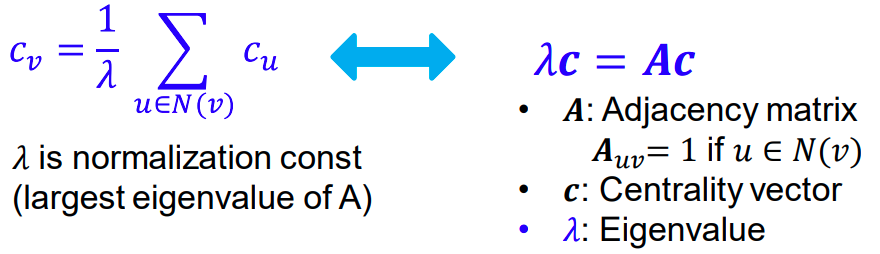
node_2

A는 adjacency matrix, 즉 인접행렬로 인접하고 있다면 1, 아니라면 0으로 나타나는 matrix입니다.
여기서 우리는 C가 A의 eigenvector라는 것 을 알 수 있습니다!

  • Betweenness centrality
    Betweenness centrality는 서로 다른 node $s$와 $t$사이의 최단경로를 그렸을 경우 그 경로사이에 $v$ 가 많이 포함 될 수록 중요하다고 여기는 방식입니다.

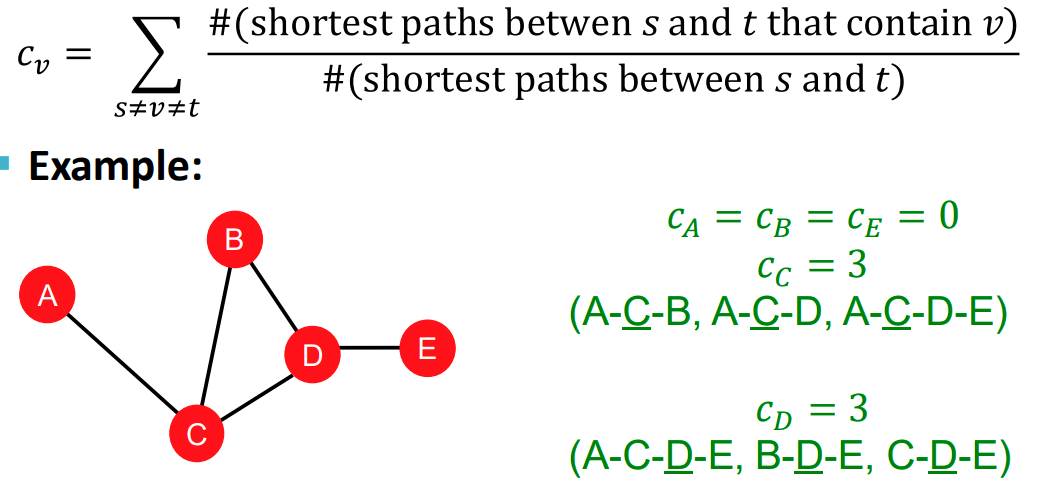
node_3

  • Closeness centrality
    Closeness centrality는 특정 node $v$에서 시작하여 서로다른 node $u$까지의 최단거리를 전부 합한 합이 작을수록 중요도를 부여하는 방식입니다.
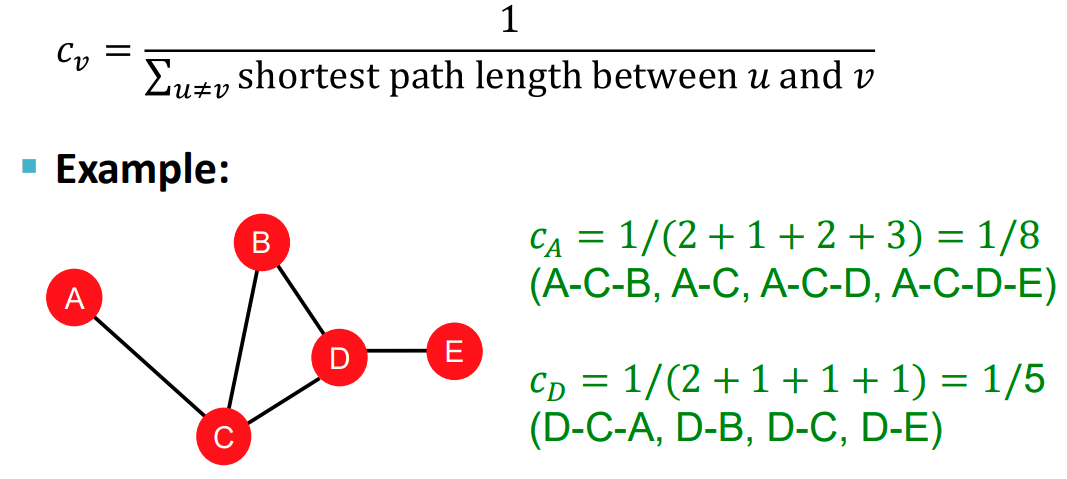
    node_4

4. Clustring coeffcient

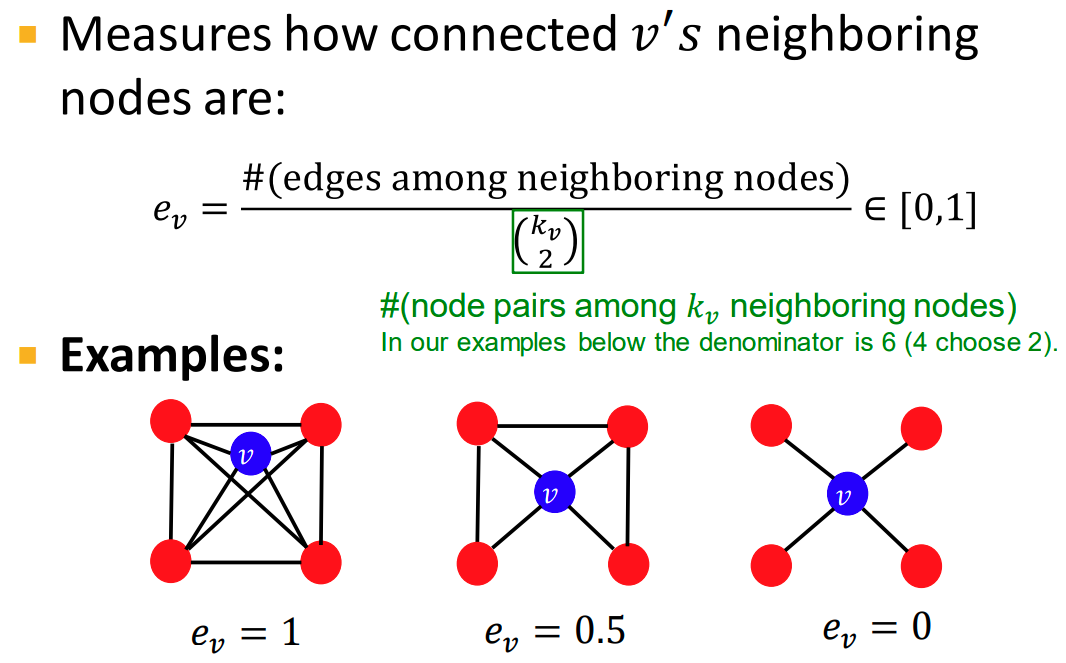
node_5

A-B, B-C라면 A-C라고 할 수 있을까요? Network에서는 항상 그렇지많은 않습니다.
이러한 성질을 추이성 이라고 하며 Clustring coeffcient는 Node $v$와 이웃한 node 2개 사이의 경로들 중 추이성을 가지는 경로의 비율을 뜻합니다.
위 그림에서는 4개의 이웃한 node들 중 2개를 골라야 하므로 $4C_{2}$, 6이 분모가 됩니다.

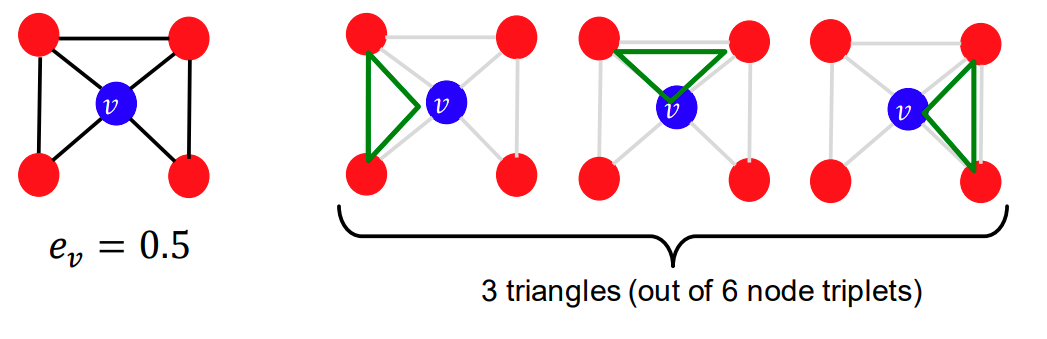
node_6
하지만 이 Clustring coefficient는 삼각형의 갯수 를 세는 것으로 쉽게 계산 할 수 있습니다.
이제 이 방식을 일반화 하기 위해 Graplet이라는 개념이 등장하기 시작합니다.

5. Graplet

Graplet은 특정 Node $u$ 를 둘러싼 network가 어떻게 생겼는지를 포착하는 개념입니다.
Graplet을 설명하기 전에 두가지 개념을 먼저 짚고 넘어가겠습니다.

먼저 Induced subgraph입니다.
Induced subgraph는 해당 그래프의 subgraph로 모든 edge를 포함하는 그래프를 뜻합니다.
node_7
위의 예제에서 not induced는 B-C를 포함하지 않았기 때문에 not indueced가 된 것 입니다.

다음으로 Isomorphism입니다.
모든 Node의 degree가 같은 경우 Isomorphic, 다른 경우 Non-isomorphic이라고 합니다.

이제 Graphlet에 대해 알아봅시다.
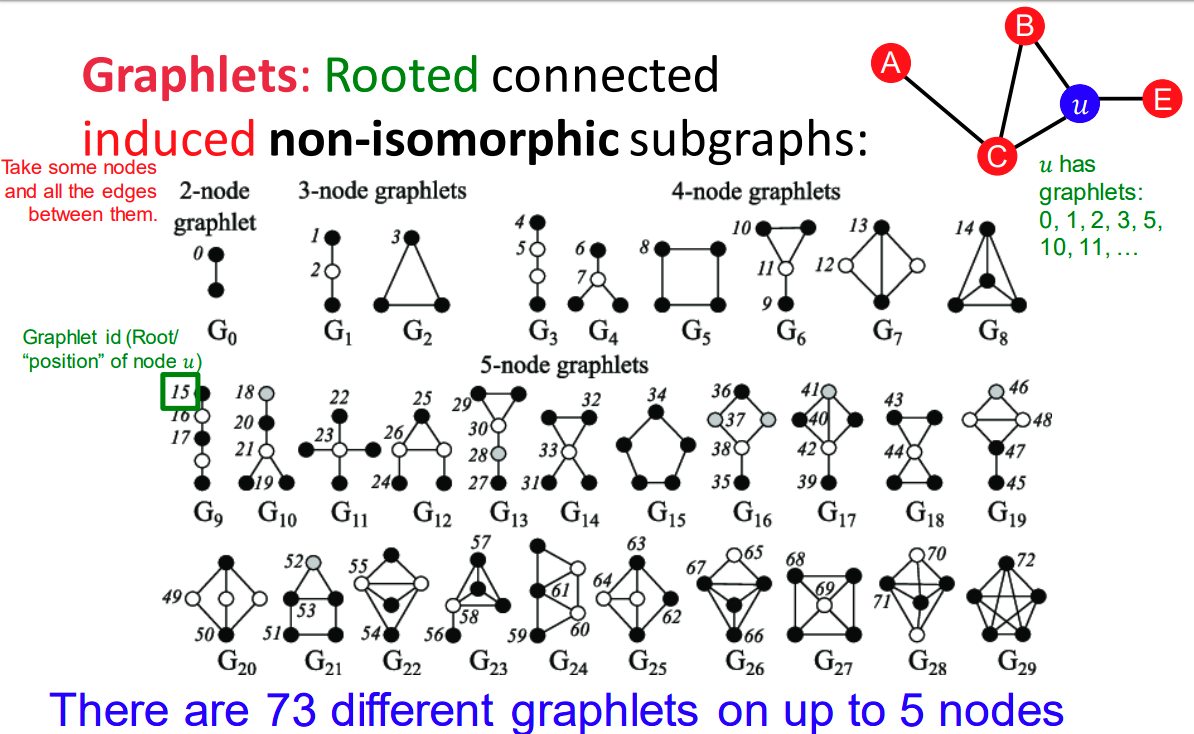
node_8
2개부터 5개의 Nodes의 경우 총 73개의 Graplets를 가지고 있으며 우리가 선택한 Node $u$의 위치에 따라 Graplet id를 이용하여 구분 할 수 있습니다.

  • Graplet Degree Vector(GDV)
    주어진 Node에서 그릴 수 있는 Graplet의 갯수를 뜻합니다.
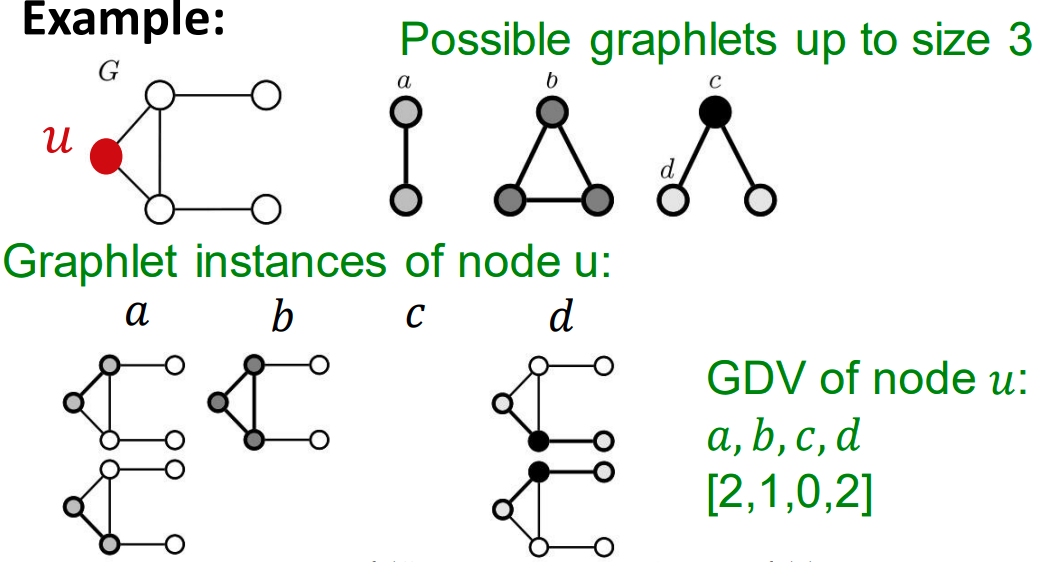
    node_9
    위 예시에서는 특정 Node $u$에서 그릴 수 있는 Graplet의 패턴은 3가지 입니다.
    또한 위 패턴에서 Graplet id는 a, b, c, d 4개이며 우리가 선택한 Node $u$가 각 id에 해당하는 패턴의 갯수를 세어주면 됩니다.

6. 정리

Node-level features는 크게 2가지로 분류 할 수 있습니다.

  • Importance base features
    • Node degree
    • Node centerality
  • Structure base features
    • Node degree
    • Clustring coefficient
    • Graplet Degree Vector

마치며

이번 포스팅에서는 Graph의 Node 관점에서 Features를 정의하는 방법에 대해 알아보았습니다.
다음 포스팅에서는 Link의 관점에서 알아볼 예정입니다.