nanoteyep

nanoteyep

DataScience trainee

© 2022

Dark Mode

Machine Learning with Graph - 2. Choise of graph representation
Jul 7, 2022
  • GNN

Choise of Graph Representation

1. Network의 구성요소

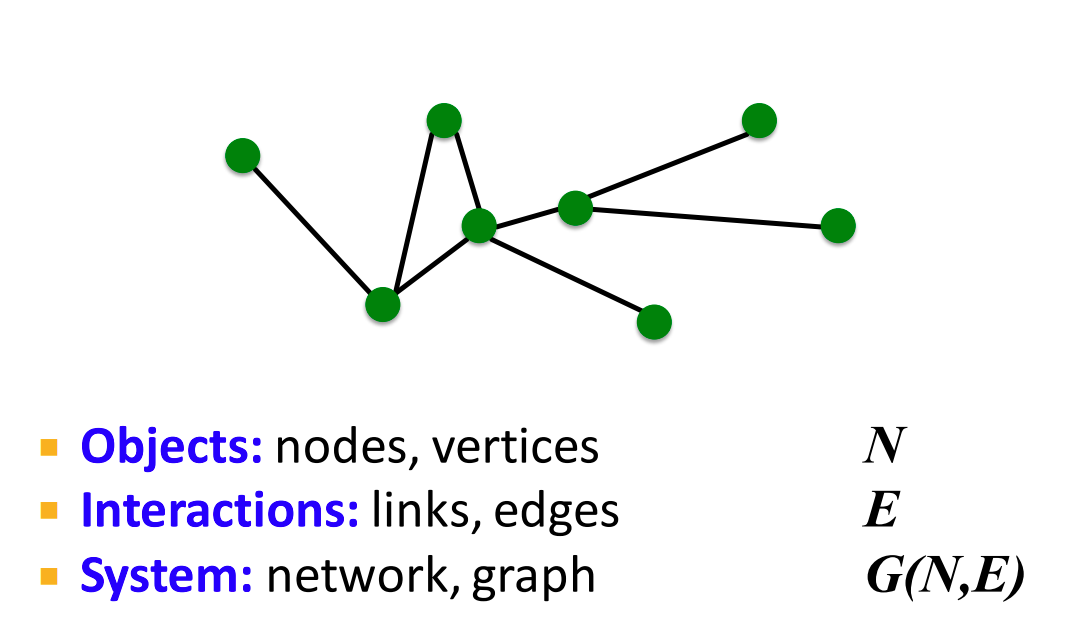
repre_1

가장 먼저 Network의 구성 요소에 대해 알아보겠습니다.
Network는 Objects, Interactions, System 으로 구성되어 있습니다.

이렇게 구성된 System을 우리는 Network라고 부르기도 하며 Graph라고 부르기도 합니다.
Objects 와 Interactions는 Node와 Edge라고 부르는 경우도 많으며 각각 N, E라고 표현하기도 합니다.
그렇기 때문에 System은 G(N, E)로 node와 edge를 포함하여 표현합니다.

2. Network의 선택

repre_2

Network는 Objects와 Interactions를 어떻게 선택 하느냐에 따라 다양한 System으로 분류됩니다.
위의 예시중 하나만 보자면 Objects를 논문으로 Interactions를 인용 관계라고 선택한다면 이 System은 citation network가 되는 것 입니다.

그렇기 때문에 Graph를 구성할 때 가장 중요한 것은 Node가 무엇인지, 그리고 Edge가 무엇인지 입니다.

3. 알아 두어야 하는 개념

  • Directed / Undirected

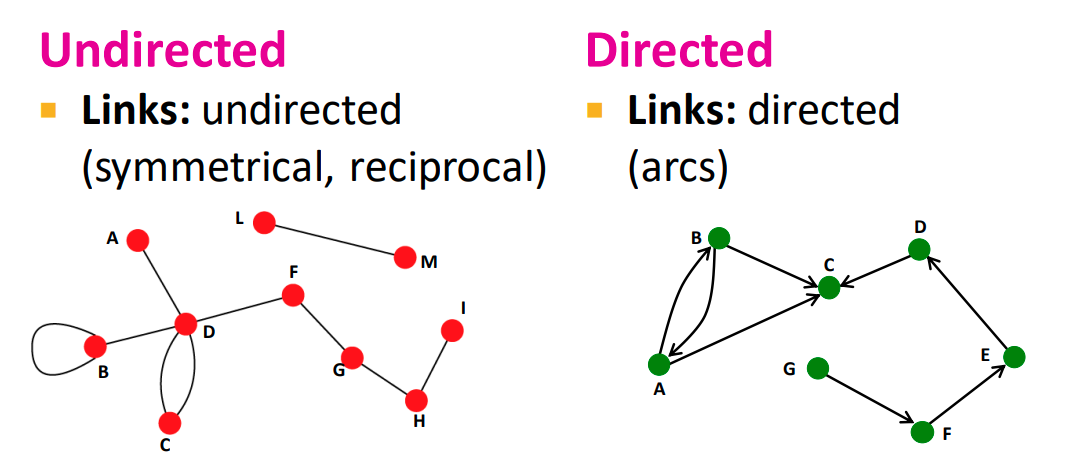
repre_3

간단하게 말해서 두 노드 사이에서 방향이 존재하는가 존재하지 않는가 입니다.

  • Heterogeneous / Homogeneous Graph

Homogeneous Graph는 모든 Node와 Edge가 같은 성질을 가진 그래프 입니다.
예를 들어 방금 설명한 citation network의 경우 모든 node는 paper이고 모든 edge는 citation인 homogeneous 한 graph입니다. 이와 반대로 Heterogeneous Graph는 node와 edge가 복수의 성질을 가진 그래프 입니다.
citation network라고 할지라도 각 node가 paper, author, date 등 다양하게 설정할 수 있으며 edge또한 이에 맞게 설정 할 수 있습니다.

많은 graph가 이러한 heterogeneous한 성질을 띄고 있습니다.

  • Node degree

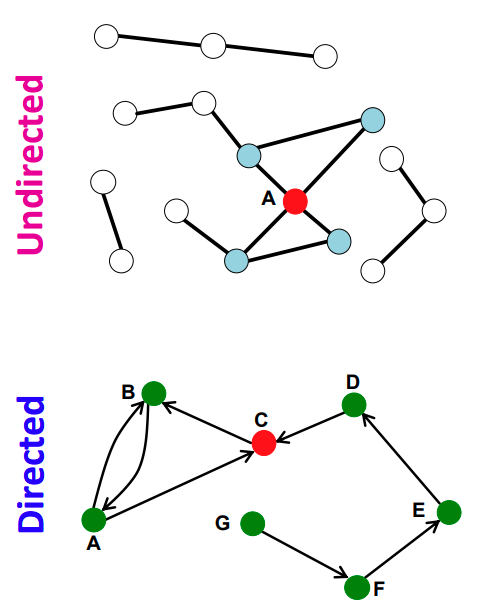
repre_4

node에 연결된 edge수를 뜻 합니다.
k라고 표현하며 Directed의 경우 in과 out으로 분리하여 사용합니다.

위 그림에서 Undirected의 node A 의 k는 4이며 Directed에서의 node C의 k는 3 이지만 K_in은 2, K_out은 1 입니다.

Avg.degree는 평균 degree를 뜻하며 Undirected의 경우 $2E\over N$, Directed의 경우 $E\over N$으로 계산 할 수 있습니다.

  • Bipartite Graph

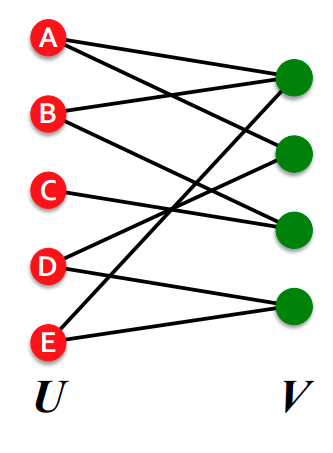
repre_5

Bipartite graph는 node 군으로 나뉘어져 edge가 서로의 node군 으로만 연결된 graph를 뜻합니다.

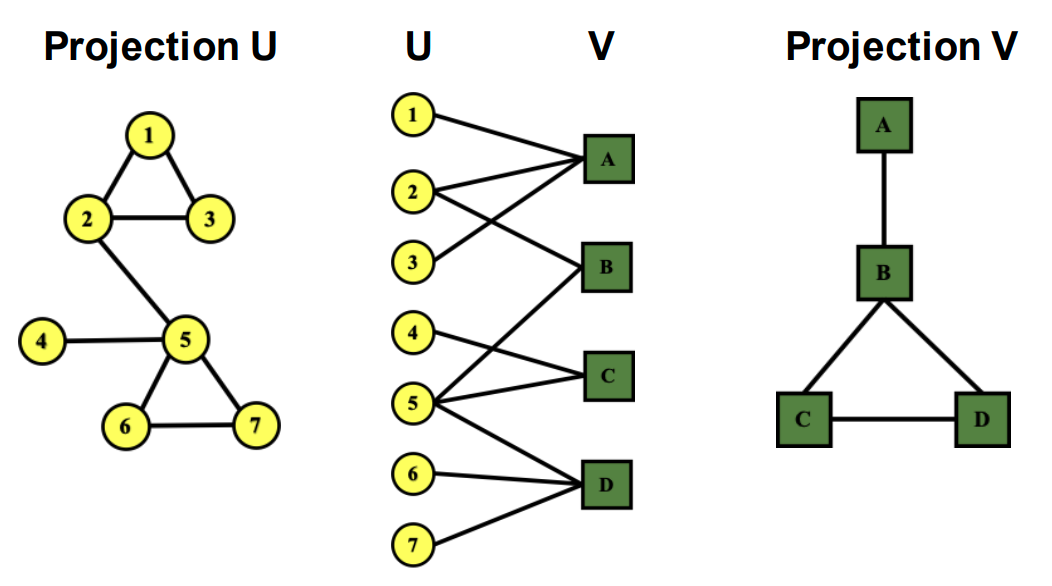
repre_6

이러한 Bipartite graph는 projection graph로 표현 할 수도 있습니다.

4. Graph를 표현하는 방법

  • Adjency matrix

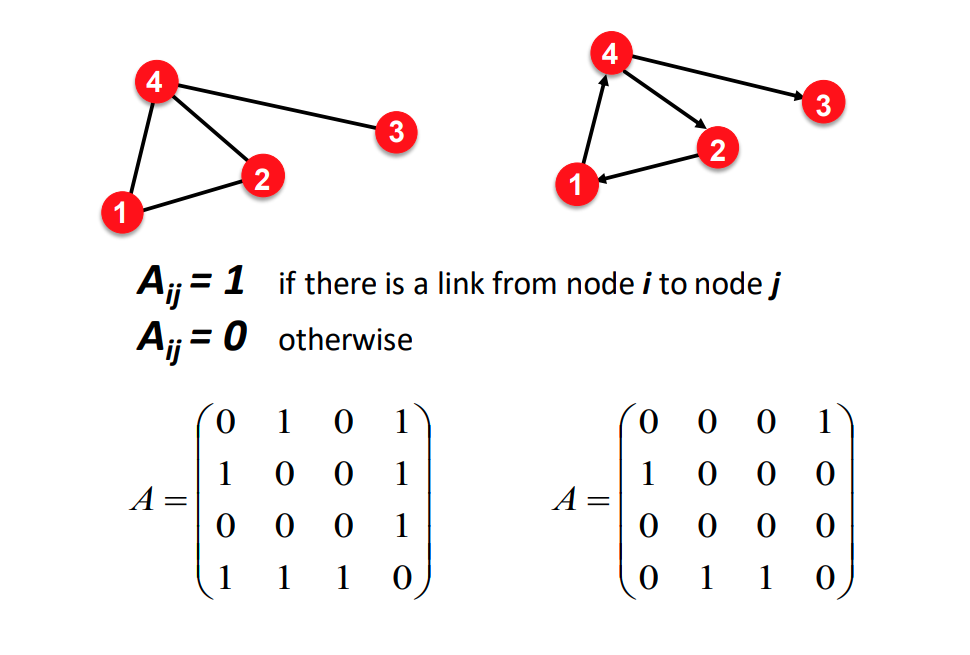
repre_7

Matrix로 graph를 표현하는 방법입니다.
Undirected와 Directed를 모두 표현 할 수 있으며 Weight, Ranking, Type이나 Sign등 다양한 option을 주어 표현 할 수 있습니다.

  • Edge List

repre_8

대부분의 Graph는 무척 Sparse, 듬성듬성 합니다.
그렇기 때문에 모든 node와 edge를 표현하는 matrix로는 표현 하기 어려운 경우가 많습니다.
이럴 때 Edge list를 사용한다면 연결된 edge만 표현하고 모든 node를 표현 하지 않아도 되기 때문에 상당히 효율적으로 graph를 표현 할 수 있습니다.

5. Connectivity

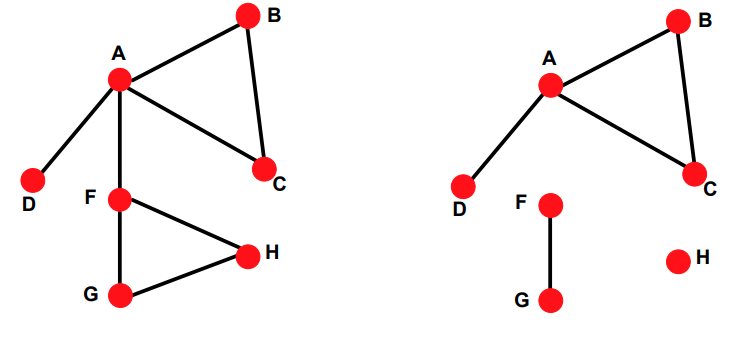
repre_9

왼쪽 그림이 Connected 된 graph이고 오른쪽이 Disconnected된 graph입니다.
또한 Connectivity는 Strongly 와 weakly로 구분 할 수 있습니다.

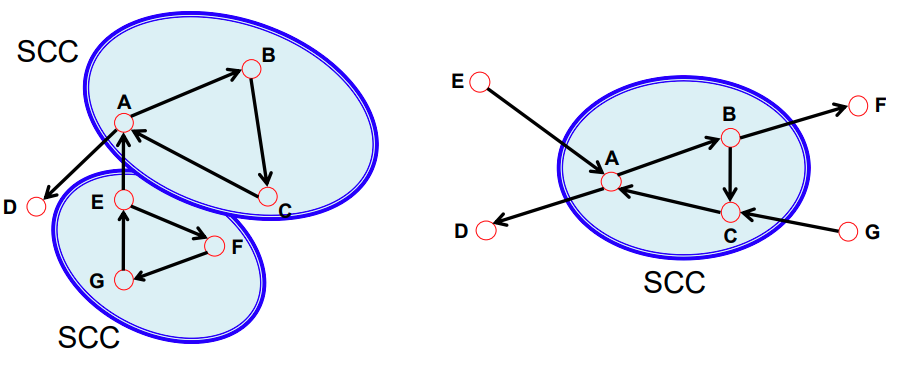
repre_10

위와 같은 graph는 Strongly Connected 된 부분을 가지고 있으며 이 부분을 Strong Connected Components(SCC)라고 합니다.

마치며

이번 포스팅에서는 graph를 구성하는 요소를 알아보고 적절한 그래프를 선택하고 표현하는 방법에 대해 알아보았습니다.
다음 포스팅 부터는 각 요소별로 알아야 하는 점과 특징들에 대해서 알아보도록 할 예정입니다.