Deep Learning - CNN
1. Convolution(합성곱 연산)
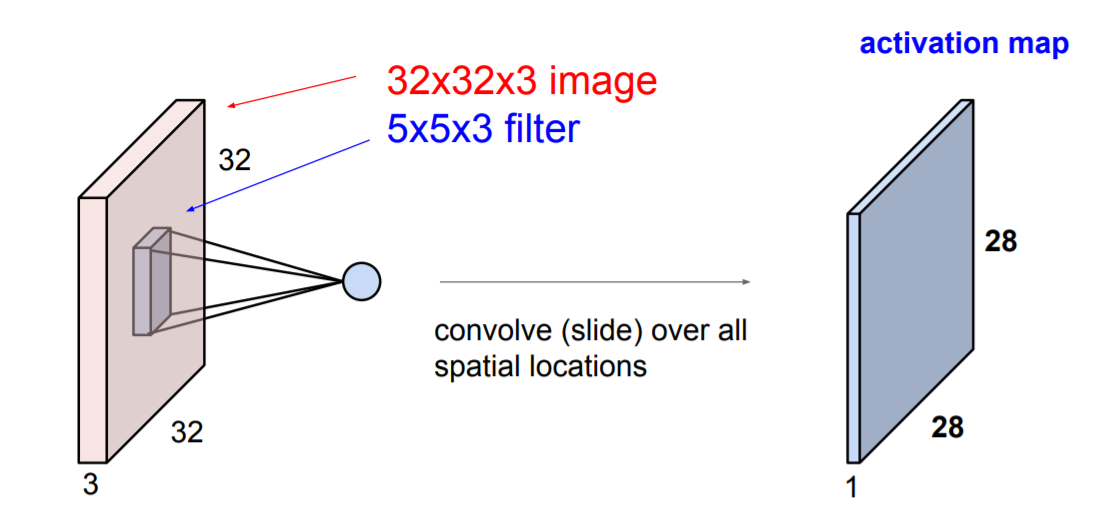
Convolution 연산은 Matrix의 dot product(내적) 연산 입니다.
이 때, 연산하는 Matrix는 원본 DATA 와 filter로 구분됩니다.
Matirx끼리의 연산이지만 dot product를 하기 때문에 결과 하나의 수치 값으로 나오게 됩니다.
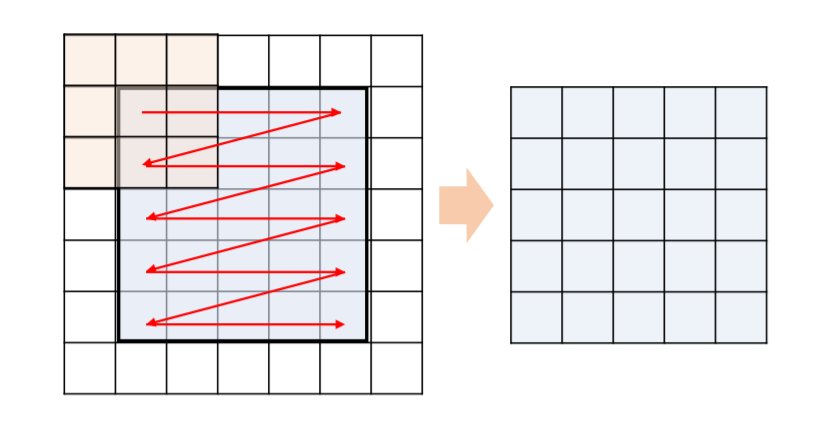
filter를 정해진 stride만큼 이동하며 원본 데이터를 전부 커버하는 것이 Convolution 연산 입니다.
1.1 padding
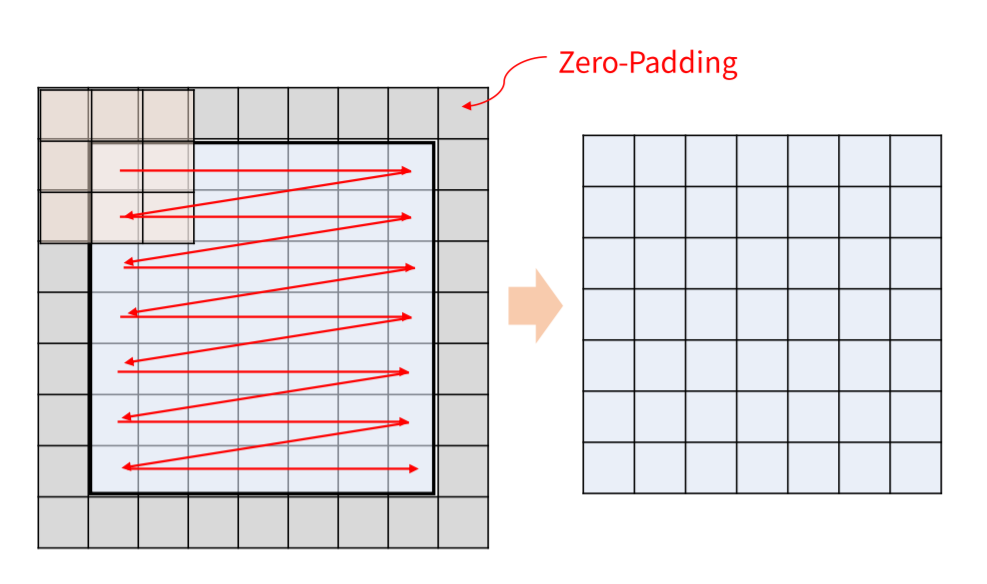
Conv연산을 하게 되면 filter의 사이즈가 1X1이 아닌이상 필연적으로 원본 DATA의 사이즈가 작아지게 됩니다.
이를 방지하기 위하여 zero-padding이라는 0으로 구성된 데이터를 이용하여 원본 DATA의 사이즈를 조금 키워주어 Conv연산 결과 사이즈가 원본과 똑같아 지도록 합니다.
1.2 stride
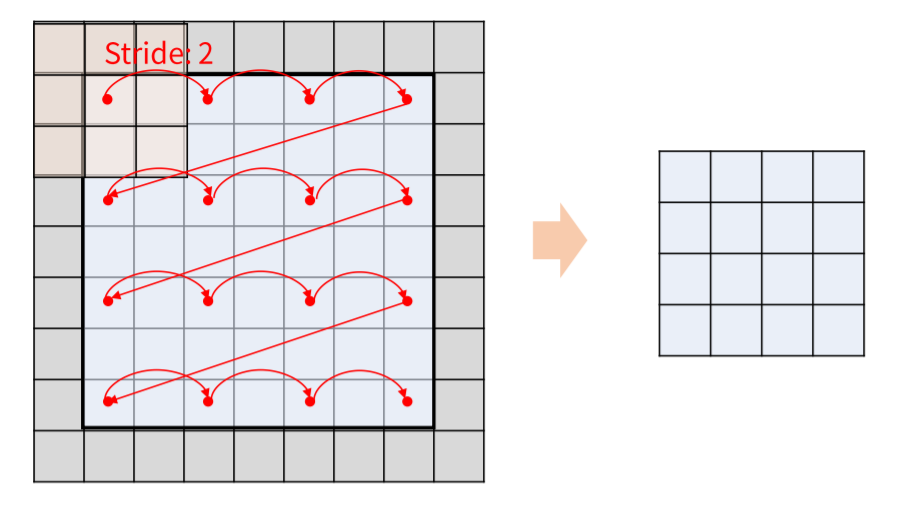
Conv연산을 할 때의 hyper-parameter이며 filter의 이동 칸수를 의미합니다.
이 값이 커질 수록 원본 DATA의 사이즈가 작아지게 됩니다.
1.3 왜 하는가
Conv연산을 하는 이유는 데이터의 위치에 따른 정보손실을 줄이기 위해서 입니다.
Convolution연산 이전에는 2차원 Matrix data, 예를 들어 이미지와 같은 데이터를 전부 1차원으로 flatten 시킨 후 Neural network에 적용하였습니다.
하지만 필연적으로 위치 정보와 같은 정보를 소실하게 되고 Conv연산을 함으로서 filter사이즈 만큼의 데이터 정보를 1X1에 함축시킬 수 있게 되었습니다.
2. pooling
- pooling 은 데이터의 사이즈를 줄이는 단계 입니다.
- 데이터의 압축이라고 생각하여도 무방합니다.
2.1 max pooling
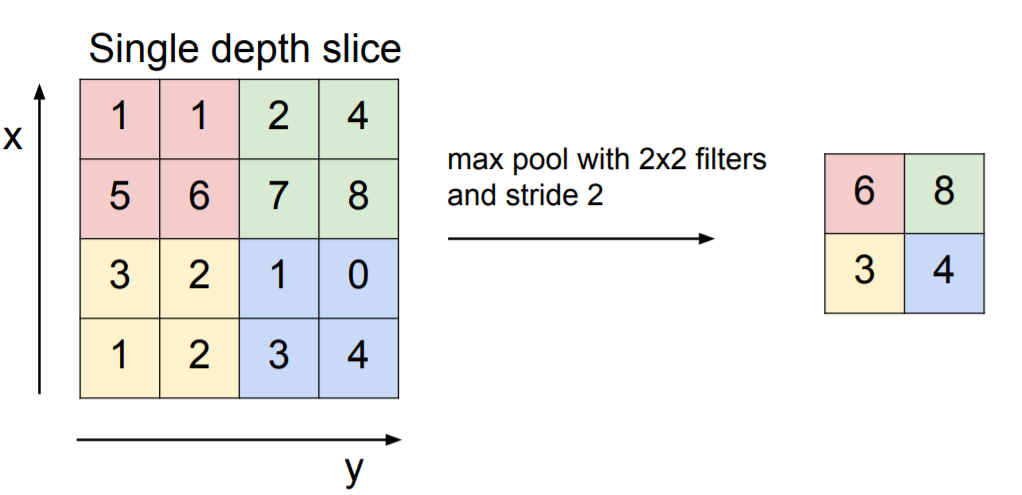
특정 filter안에서 가장 큰 값을 출력하는 pooling기법입니다.
모든 pooling기법에서도 마찬가지지만 2X2로 pooling할 경우 원본 사이즈가 절반이 되어 출력됩니다.
max pooling을 하는 이유는 conv연산을 하게 되면 filter에 걸맞는 특징이 출력되는데 이 특징이 가장 두드러지는 data를 추출한다는 것 입니다.
대부분의 CNN에서 이 max pooling을 사용합니다.
2.2 mean pooling
평균값을 출력하는 pooling기법입니다.
잘 사용하지는 않습니다.
3. CNN Architectures
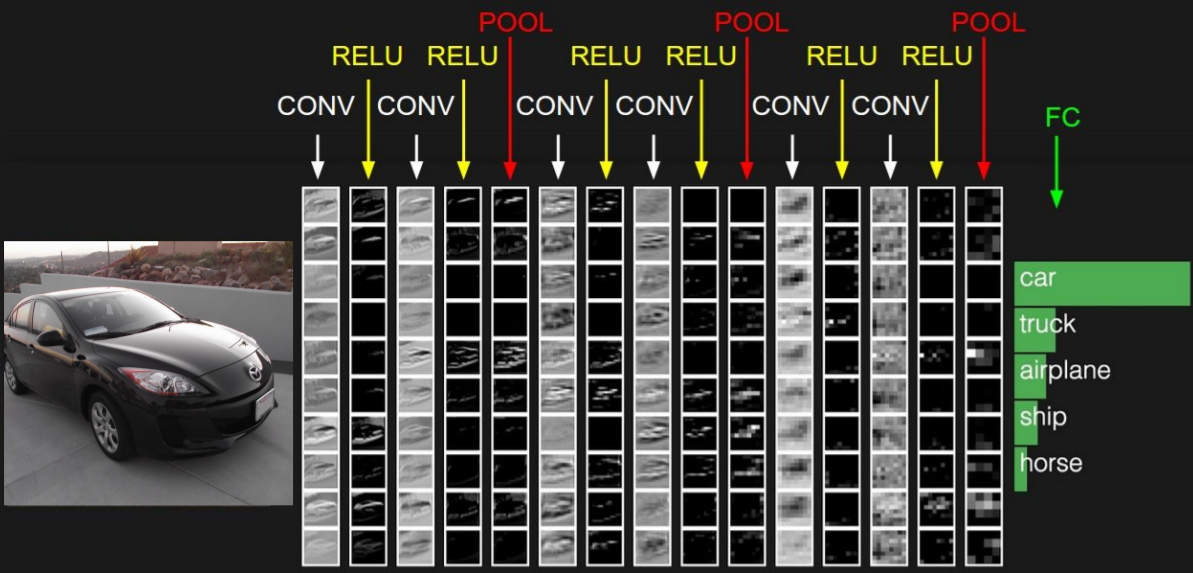
위 사진과 같이 Conv layer, pooling layer, FC layer 등으로 이루어진 구조 입니다.
FC는 Fully Connected의 약자로 Neural Network구조이며 layer에 진입하기 전에 flatten단계를 거쳐야 합니다.
CNN 학습이란 Conv layer에서 생성되는 filter, FC layer에서 생성되는 weight를 학습하는 과정이며 Neural Network와 마찬가지로 pack propagation을 통해 loss function이 최소화 하는 방향으로 업데이트가 진행됩니다.
3.1 Image Net
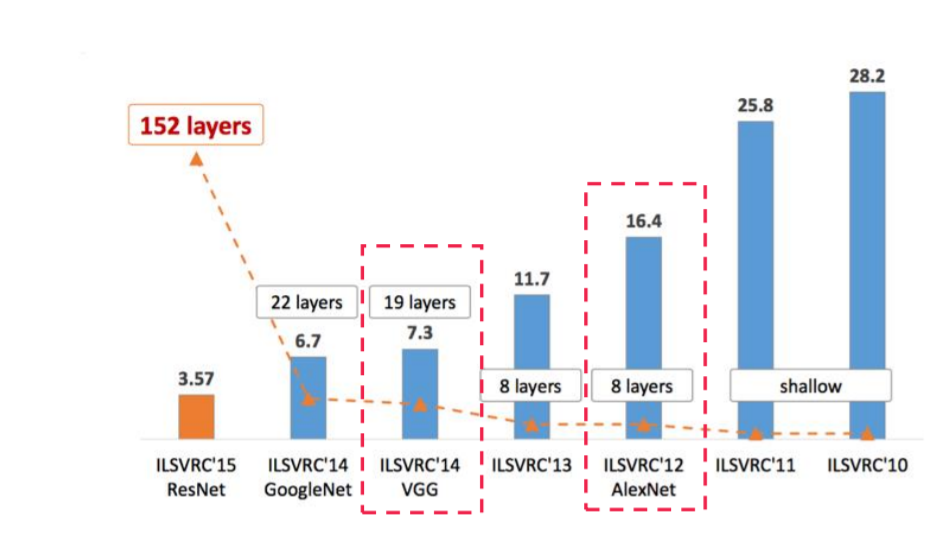
Image Net은 Computer Vision을 겨루는 대회이며 현재는 kaggle로 합병되었습니다.
위 그래프는 매년 Image Net우승 architectures이며 y축은 에러율을 의미합니다.
CNN 구조를 이해하기 위해 AlexNet과 획기적으로 error를 줄인 ResNet에 대해 알아보고자 합니다
3.2 AlexNet
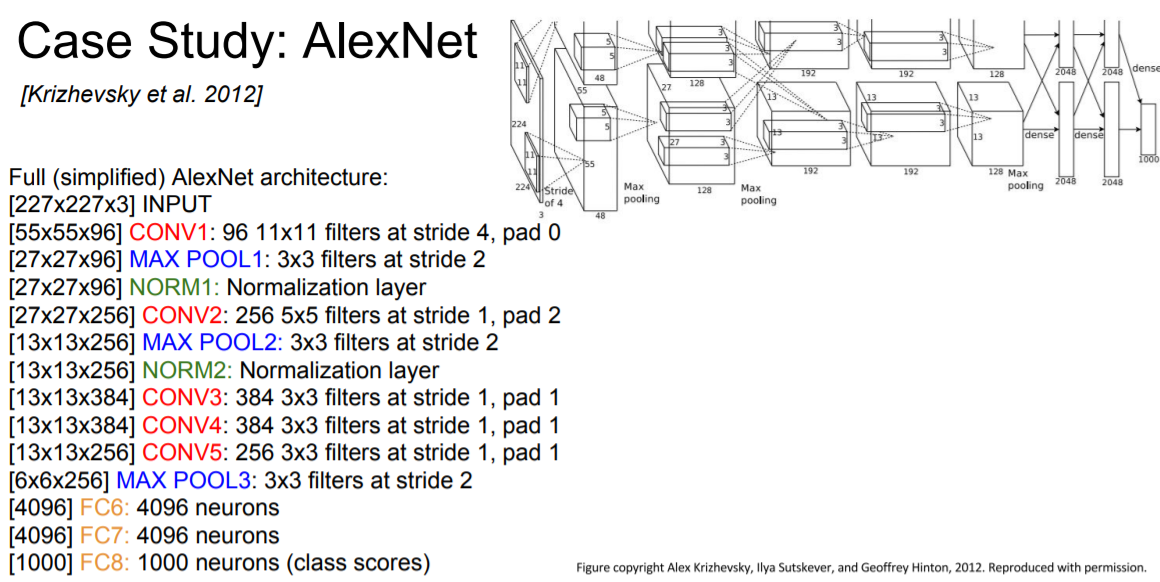
227X227X3의 이미지 데이터를 input으로 하는 CNN구조입니다.
X3은 채널이며 컬러 이미지의 경우 RGB로 나누어진 3개의 채널, 흑백 이미지의 경우 2개의 채널로 구성됩니다.
Conv layer 의 경우 input channel은 이전 데이터의 channel과 동일해야하지만 output channel의 경우 hyper-parameter로 사용자가 직접 지정해 주어야 합니다.
데이터 사이즈에 유의하며 천천히 구조를 살펴본다면 쉽게 이해 가능할 것 입니다.
AlexNet의 경우 무척 오래된 구조이기 때문에 당시 메모리 사이즈가 부족하여 데이터를 두개로 쪼개 각기 다른 GPU에서 연산하였기 때문에 구조도에서 반으로 쪼개진 것 처럼 보입니다. 하지만 동일한 연산을 두개의 GPU에서 행하기 위해 분산시켜준 것이기 때문에 기본적으로 같은 구조 입니다.
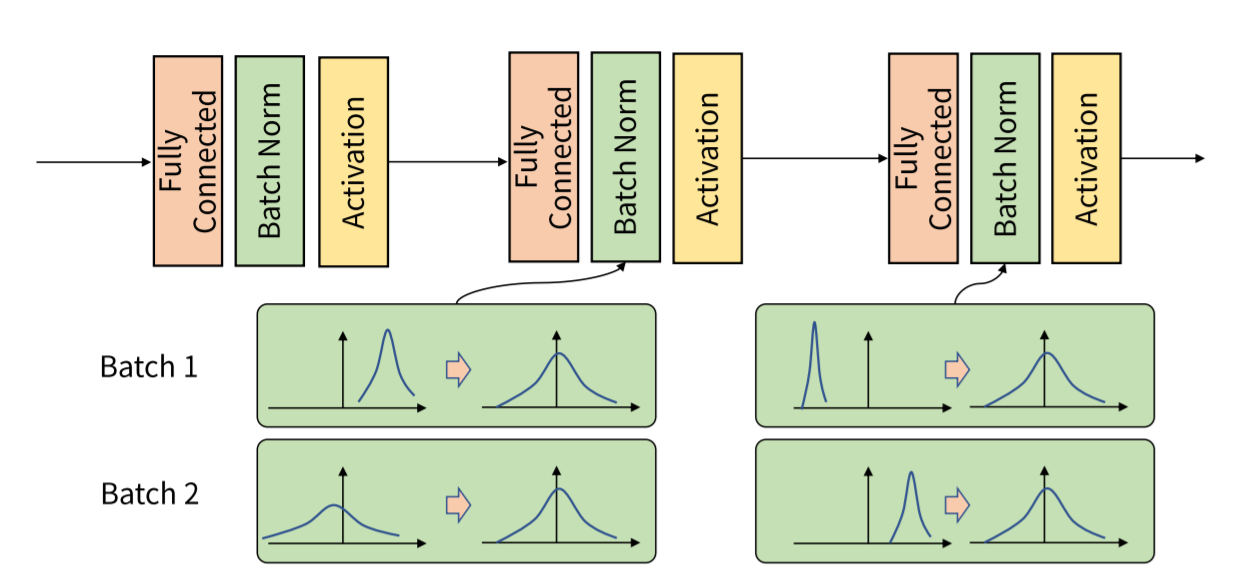
여기서 처음나온 normalization이란 위와 같이 분포도를 재 조정해주는 역할을 합니다.
normalization을 하지 않고 activation function, 주로 ReLU에 넣게 된다면 음으로 치우쳐진 데이터는 대부분 소실될 것이고 양으로 치우쳐진 데이터는 그대로 출력되어 아무 의미를 가지지 않을 것 입니다.
그렇기 때문에 activatio function이전에 normalization term을 가져 데이터를 보정해주는 것 입니다.
3.3 ResNet
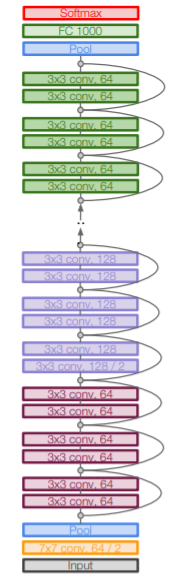
152개의 layer로 구성된 ResNet입니다.
ResNet이전의 구조들은 layer가 깊어질수록 계속된 미분으로 인해 Gradient vanising이 발생하게 하지만 ResNet은 Residual block 을 사용하여 이를 방지합니다.
Residual block은 input값인 x와 layer를 거치고 나온 F(x)를 서로 더한 값을 다음 block의 input으로 주는 방식입니다.
이렇게 더해주는 것으로 초기 layer들의 Gradient가 소실되지 않고 끝까지 전달되며 layer를 더욱 깊게 쌓는 것이 가능하게 되었습니다.
ResNet이후 deep한 layer가 더욱 뛰어난 성능을 가지는 것을 알게 되었습니다.
마치며
이 외에도 더욱 많은 CNN구조가 존재하지만 이 포스팅에서는 다루지 않겠습니다. 어디까지나 CNN구조를 이해하고 구조를 보고 재현 할 수 있는 것에 초점을 맞추었습니다.
