nanoteyep

DataScience trainee

Road to Datascientist - 27. 신경망 모형

Aug 27, 2021

DataScience
ML

Neural Network

1. 신경망 모형(Neural Network)이란?

신경망 모형은 인간의 신경세포, 즉 뉴런의 구조를 모델링 하는 학습입니다.
하나의 뉴런을 perceptron 이라고 표현하며 B에 해당하는 부분입니다.
또한 이런 여러개의 perceptron을 합쳐 여러개의 layer를 구성함으로서 뉴런의 결합인 synapse를 모델링합니다.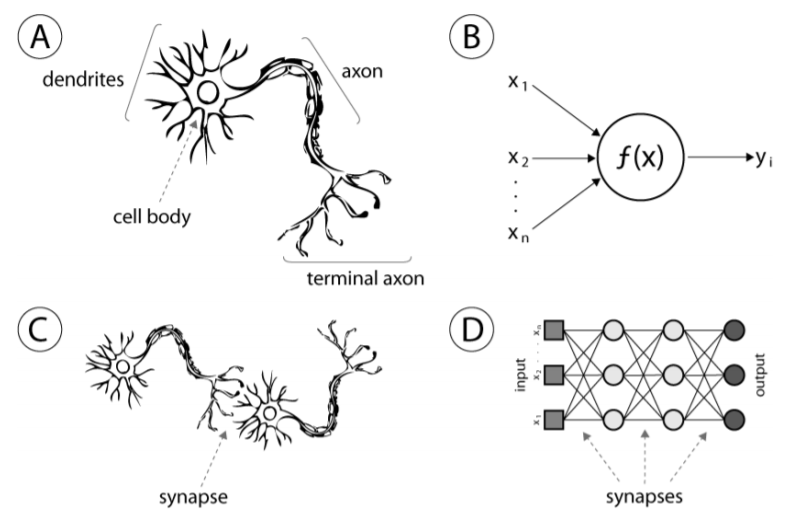
Perceptron

nn_2

nn_4

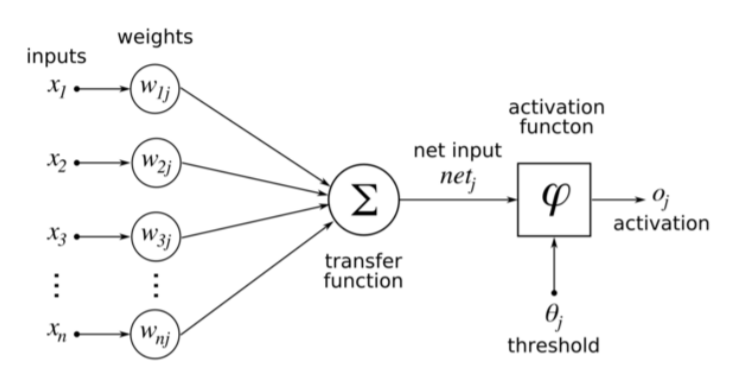
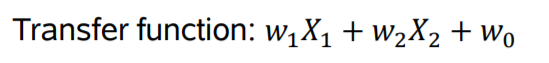
perceptron은 하나의 뉴런을 구조화 시킨 모델입니다.

입력데이터 X를 받으며 이에 대한 weights, weights는 선형회귀 모델에서의 $\beta$와 같은 역할을 합니다.

input과 weights를 계산하여 결과값을 내며 이것을 activation function에 적용 시킨 후 또 다른 perceptron의 input값으로서 적용시킵니다.

activation function

nn_5

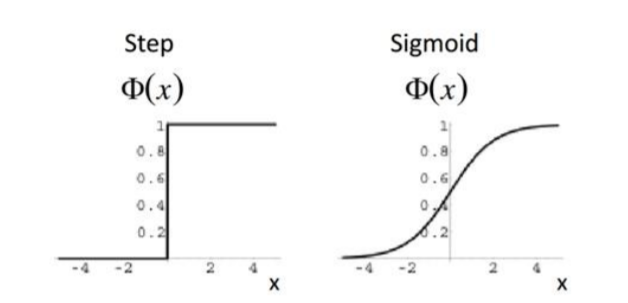
activation function은 hidden layer를 의미있게 쌓아주는 역할을 합니다.

step방식과 sigmoid방식은 초창기 neural network에서 많이 쓰이던 activation function으로 몇가지 문제점을 안고 있습니다만 추후에 설명하도록 하겠습니다.

Multi Layer Perceptron

nn_3

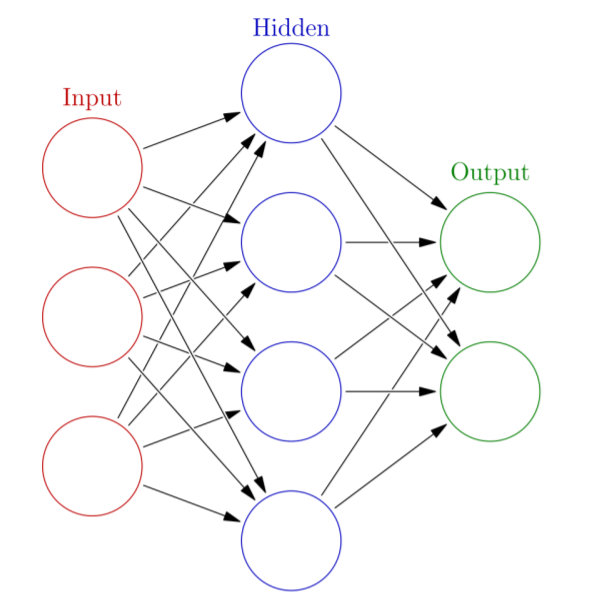
perceptron이 하나의 뉴런을 의미한다면 Multi Layer Perceptron은 뉴런의 결합, synapse를 의미합니다.

위 그림에서는 하나의 Hidden layer가 존재하며 이는 4개의 perceptron으로 이루어져 있습니다.

또한 그렇게 나온 Output layer는 총 2개의 perceptron으로 이루어져 있습니다.

Playground tensorflow

Playground_tensorflow

nerual network를 이해하는데 많은 도움을 주는 사이트 입니다.

직접 간단하게 perceptron을 추가하고 조정하며 모델을 돌려볼 수 있습니다.

2. 알고리즘

nn_6

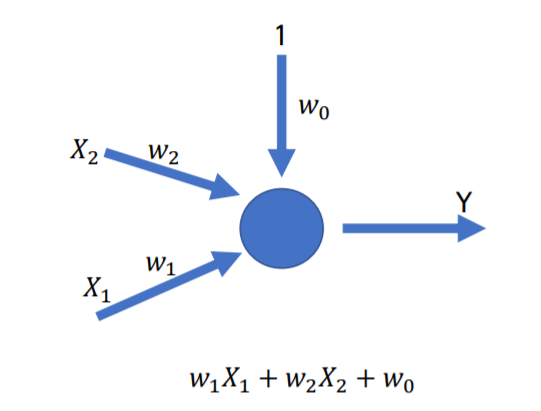
하나의 perceptron은 위와 같은 구조로 연산을 하게 됩니다.

처음부터 weight가 정해져있기 때문에 학습을 위해서는 weight를 업데이트 해주며 학습을 진행해야 합니다.

nn_7

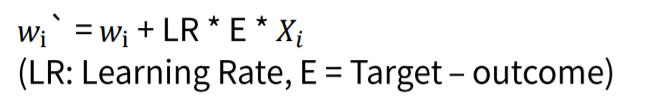
그 방법이 바로 Gradient descent(경사 하강법)입니다.

E는 실제 Y와 비교한 error이며 LR은 직접 설정해 주어야 하는 학습률 입니다. LR이 너무 작으면 weight의 변화가 작기 때문에 수렴하는데 시간이 오래걸리며 너무 크다면 정확한 해를 찾기 힘듭니다.

OR연산 구축

nn_8 nn_9

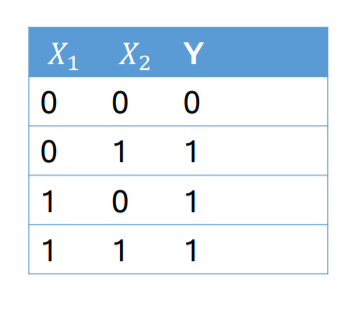
이번엔 OR연산을 perceptron을 이용하여 구축해 보도록 하겠습니다.

X와 Y의 데이터와 초기 조건이 다음과 같을때 부터 시작합니다.

nn_10

첫 행의 연산입니다. X 값이 전부 0일 경우 $\hat Y$이 -0.4, 즉 0보다 작기 때문에 step function에 의해서 0이 출력되게 됩니다.

$\hat Y$ 과 Y가 같기 때문에 E, error는 0이 나오며 업데이트 된 weight에 변화가 없습니다.

nn_11

두 번째 행의 연산입니다. $\hat Y$이 0이 나왔으나 Y가 1이기 때문에 E = 1 이며gradient의 업데이트가 일어납니다.

nn_12

세 번째 행의 연산입니다. 업데이트 된 gradient를 사용하였으나 다시한번 error가 생겼으며 또다시 gradient를 업데이트 합니다.

nn_13

마지막 행의 연산입니다. 연산이 제대로 되었기 때문에 Error가 발생하지 않았으며 gradient는 업데이트 되지 않습니다.

nn_14

마지막으로 업데이트 된 gradient를 이용하여 다시 첫 행부터 연산을 시작합니다.

업데이트 된 연산이 첫번째 행에서도 잘 작동하기에 업데이트를 하지 않고 다시 다음행으로 넘어갑니다.

nn_15

두 번째 행 또한 연산이 제대로 되었습니다.

nn_16

세 번째 행 또한 연산이 제대로 완료 되었습니다.

마지막 항에서 업데이트 된 gradient이기 때문에 마지막 항 또한 제대로 된 연산이 완료 될 것 입니다.

따라서 현재 마지막으로 업데이트 된 gradient가 최적의 gradient이며 좀 더 복잡한 연산일지라도 이 과정을 계속 반복하면서 최적의 해를 찾는 연산이 Neural Network입니다.

Backpropagation(역전파 알고리즘)

nn_17

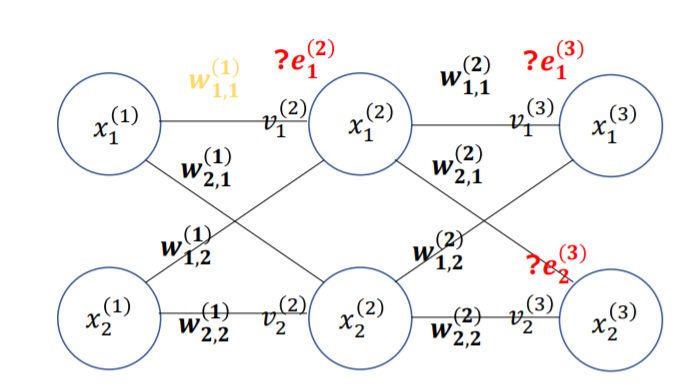
Backpropagation은 단일의 Multi Layer perceptron을 학습시키기 위한 방법입니다.

단일 perceptron의 경우 Logestic regression과 같이 선형으로 학습하기 때문에 선형으로 구분 할 수 없는 데이터는 학습 할 수 없습니다.

그렇기 때문에 사용하는 것이 Multi Layer Perceptron이며 문자들의 의미는 다음과 같습니다.

아래첨자는 지금 까지와 마찬가지로 각기 다른 데이터를 의미합니다.

위첨자는 Layer의 층을 의미합니다.

weight의 아래첨자는 목적지, 출발지를 의미합니다. 즉 w_{2, 1} 는 x₁에서 x₂로 가는 perceptron의 weight를 의미합니다.

nn_20

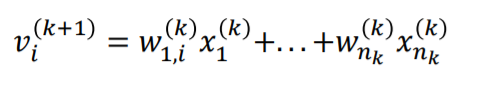
$\nu$는 activation function에 들어가기 전 출력값을 의미합니다. 즉 단일 perceptron에서 연산한 결과값입니다. 이 값이 activation function에 들어 간 후 결과 값이 다음 perceptron의 x로서 기능합니다.

nn_18 nn_19

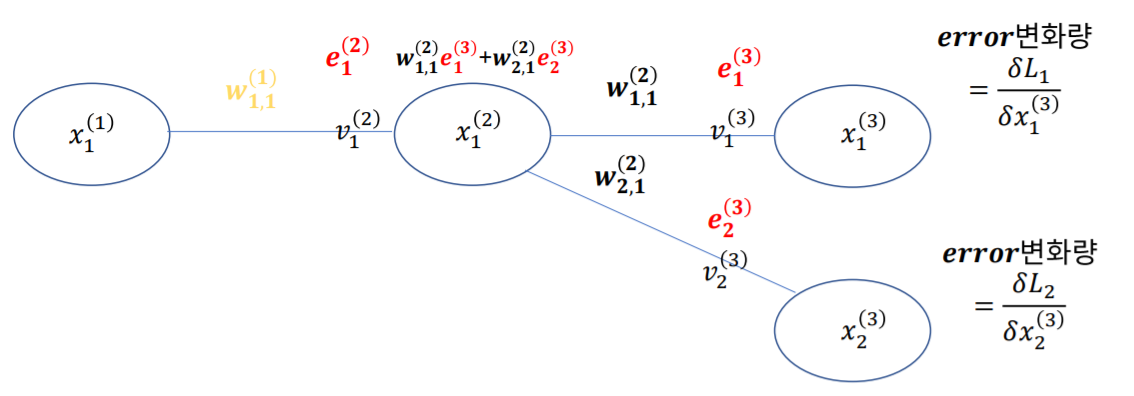
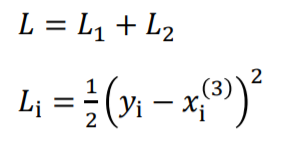
L은 에러값입니다. 하지만 이 L은 바로 업데이트에 사용하지 않고 x로 미분한 후에 업데이트를 위한 에러로 사용합니다. 그 값을 e라고 합니다.

nn_21

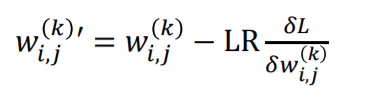
업데이트를 위한 식입니다. 단일 perceptron과 다른점이 없지만 이전 layer의 perceptron을 업데이트 하기 위해 다음 layer의 error값을 넘겨주기 때문에 backpropagation이라고 불립니다.

nn_22 nn_23 nn_24

nn_25

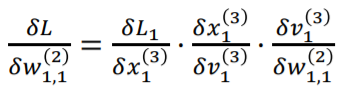
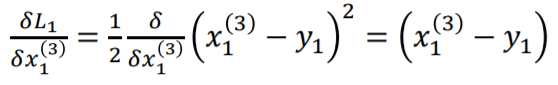
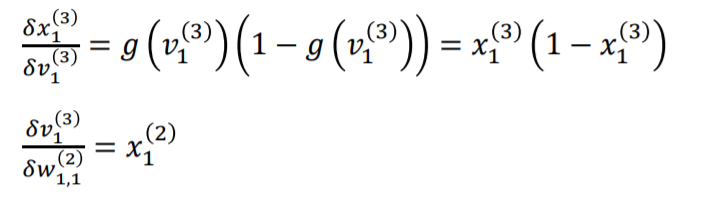
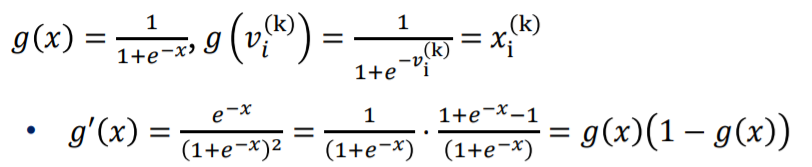
x1을 v1으로 미분하는 식의 g(x)는 sigmoid function입니다.

sigmoid function을 activation function으로 사용하는 이유는 미분하였을 경우 자기 자신을 이용한 식이 나오기 때문에 미분하기 쉽기 때문입니다.

nn_26

따라서 정리해 보면 위와 같은 식으로 업데이트 됩니다.

nn_27

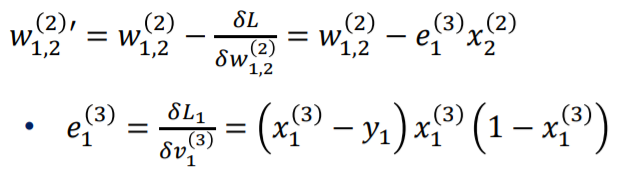
같은 식으로 w _1,2 또한 업데이트 할 수 있습니다.

위와 업데이트된 weight는 첫 레이어로 전파되어 새롭게 업데이트를 진행 할 것이며 이와 같은 과정이 계속 반복됩니다.

3. 한계점

Gradient vanising

nn_28

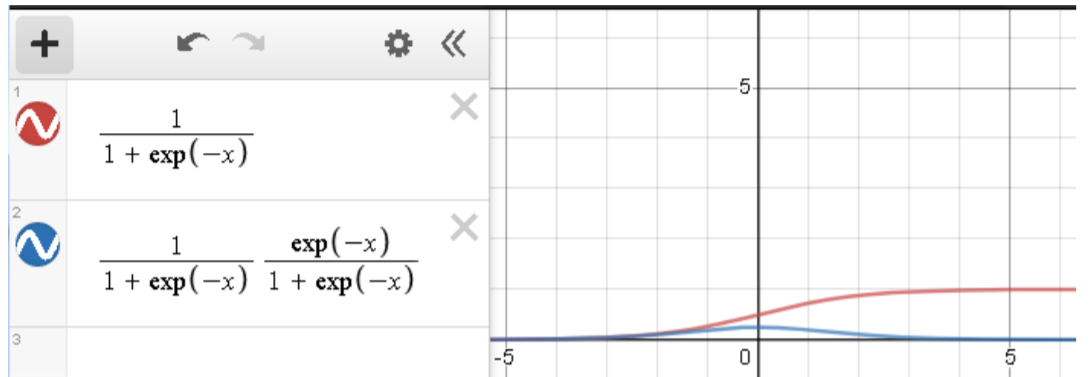
activation function으로 쓰인 시그모이드 함수의 한계입니다.

미분한다면 자기 자신의 식으로 나오기 때문에 편해서 사용하였으나 값이 클 경우 0으로 수렴하는 특징이 있습니다.

즉 데이터의 수치가 클경우 데이터가 소멸되는 효과를 가져오기 때문에 Neural Network의 한계로 지적되고 있습니다.

Local minimum

nn_29

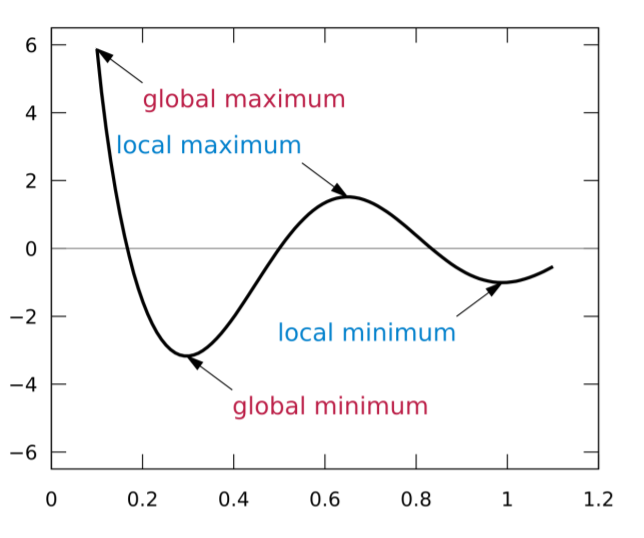
미분하여 최솟값을 구한 값이 global minimum이 아닌 local minimum일 가능성이 있습니다.

Overfitting

weight가 크다면 overfitting이 일어난 다는 단점이 있습니다.

4. 극복

ReLU

nn_30

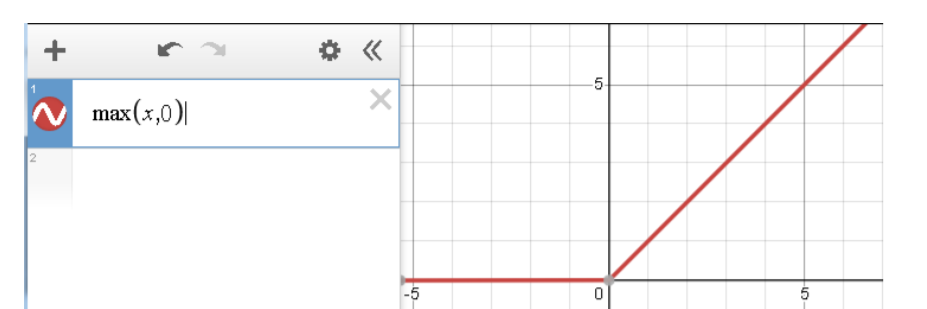
Gradient vanising을 해결하는 방법입니다.

activation function을 시그모이드 함수 대신 위와 같은 ReLU를 사용하여 해결하였으며 훨씬 간단하기 때문에 연산속도가 빠릅니다.

또한 Gradient vanising이 해결되어 Local minimum을 구하는 현상이 완화되었습니다.

Boltzmamn machine

pre-training을 통해 Global minimum근처에서 w의 초기값을 정하는 방식 입니다.

Y를 제거하여 비 지도학습을 진행하여 w의 초기값을 정하면 Global minimum근처에서 연산을 진행하기 때문에 구한 최솟값이 global minimum일 가능성이 높아지게 됩니다.

Drop out

nn_31

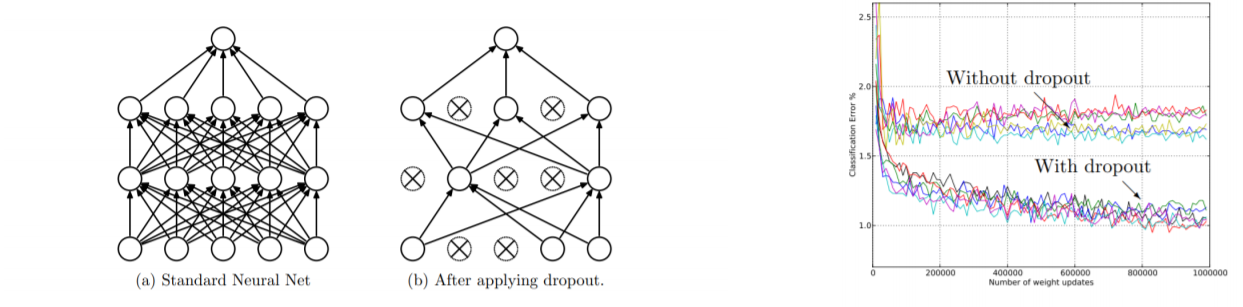
너무 많은 노드가 있을 경우 과적합이 일어날 확률이 높습니다.

그렇기 때문에 Hidden layer의 node를 임의의 확률에 따라 남기며 이때의 확률은 0.5에서 1사이를 권장합니다.

랜덤하게 node가 사라졌기 때문에 과적합 문제도 완화되며 계산 속도 또한 증가하게 됩니다.

마치며

이번 포스팅에서는 Neural Network에 대해 알아보았습니다. Neural Network는 초기 여러 문제를 안고 있었지만 지금은 다양한 문제가 해결되어 딥러닝의 기반이 되고 있습니다. 또한 기존의 ML연산과는 다르게 계속해서 학습을 진행하며 멈추기 전까지 최적의 해를 계산하는 특징까지 지니고 있습니다. 그렇기 때문에 playground_tensorflow사이트에서 node와 layer를 늘려보면서 시각적으로 그 의미를 파악해 보길 바랍니다.