Decision Tree
1. Decision Tree 란?
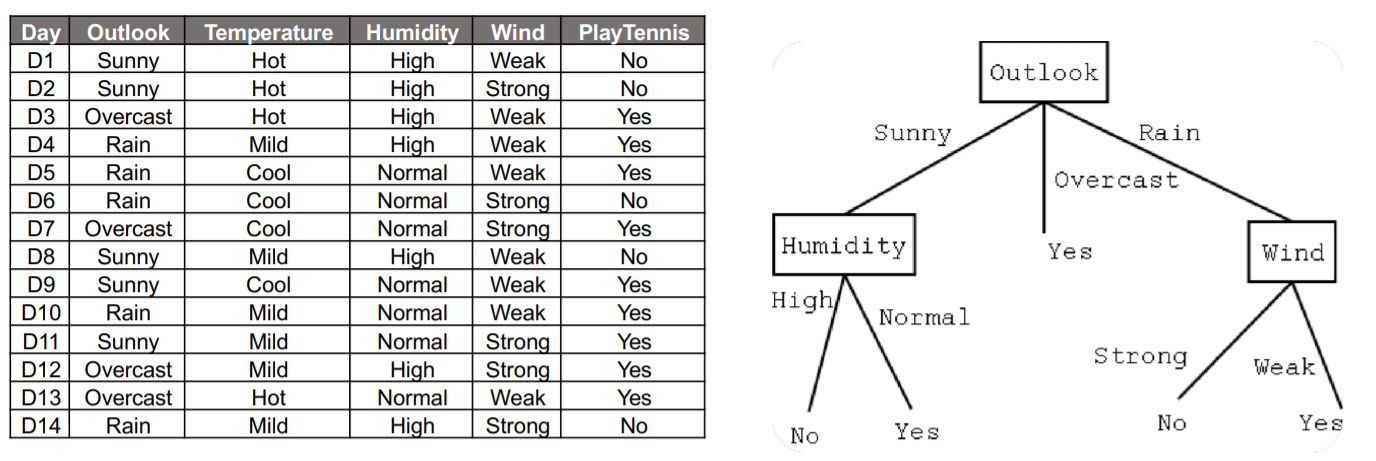
Decision Tree란 위의 그림과 같이 변수들을 기준으로 데이터를 분류하고 Y를 추정하는 분류(classify)모델 입니다.
하지만 Regression tree또한 존재하며 Regression tree는 Decision tree와 같은 방식을 사용하는 회귀(regression)모델 입니다.
2. 수학적 개념
- Entropy(엔트로피)
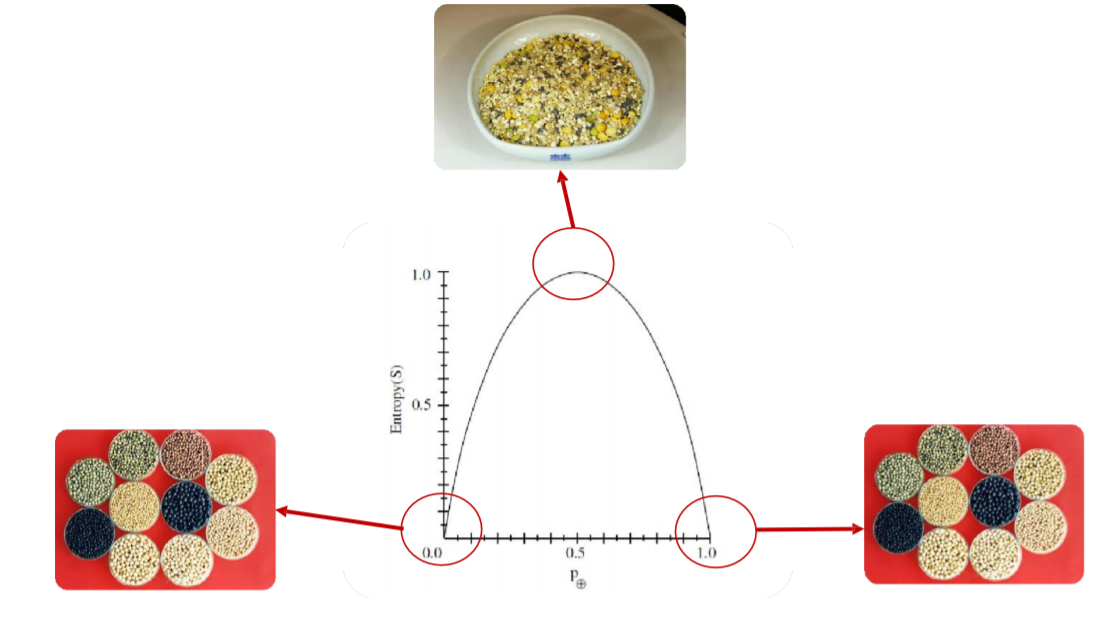
Entropy는 간단하게 복잡도를 나타내는 용어 입니다.
양 끝 entropy가 0가 되는 부분은 완벽하게 특정 상태로 분류가 되어 있는 상태입니다.
가장 entropy가 높아진 부분은 복잡도가 가장 높은 상태입니다.
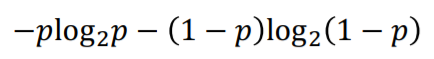
이러한 entropy를 수식으로 나타내면 위와 같이 정의됩니다.
- Information Gain
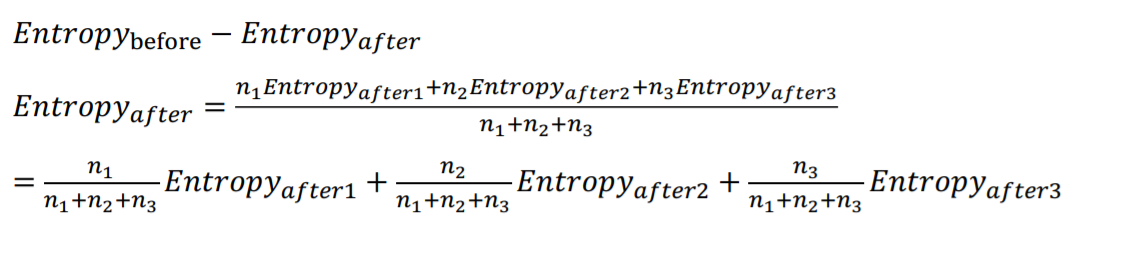
Information Gain은 이전 entropy - 이후 entropy입니다.
첫 노드 이후에 여러가지로 분할되었다면 위와 같이 평균 entropy를 구하여 계산 합니다.
3. 노드 구성
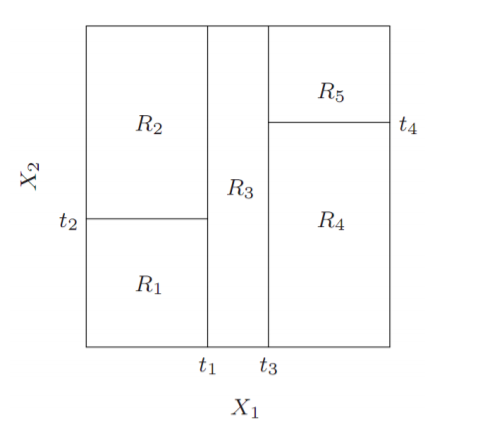
Decision tree는 features에 따라 X가 가질 수 있는 영역을 블럭으로 나누게 됩니다.
이 때 나누어진 영역안에서 Y의 특성을 통하여 Y를 추정하는 방식입니다.
그렇다면 이 영역은 어떻게 나누는지 알아 봅시다.
- 범주형
X가 범주형 변수일 경우 간단하게 범주별로 나누어 주면 됩니다.
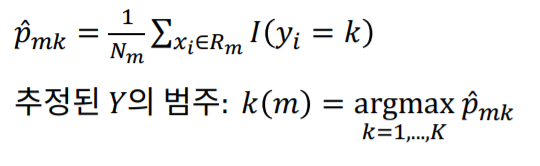
p는 특정 영역에서 그 범주가 존재할 확률입니다.
이 때 $\hat y$는 p가 가장 커지는 범주로 추정합니다.
- 연속형
연속형일 경우 여러개의 영역을 임의로 나누어 줍니다. 이 때 depth, 즉 몇번 분할 할지는 사용자가 정해주게 됩니다.
이때 영역을 나누는 기준은 아래 mearsure를 기준으로 분류합니다.
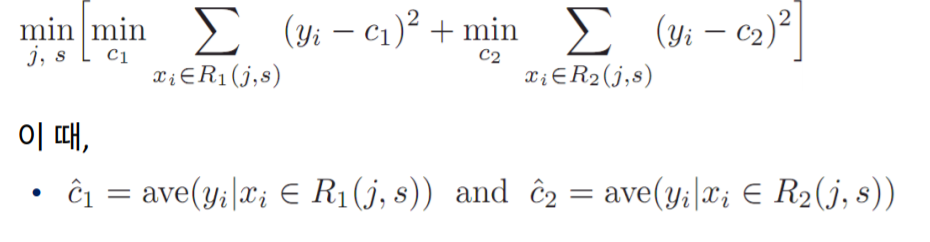
이와 같은 measure가 가장 낮아지는 방향으로 분류합니다.
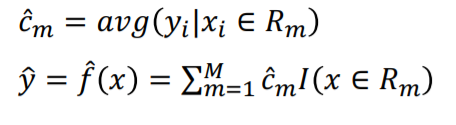
영역이 결정된다면 위와 같이 y를 추정합니다.
c는 결정된 영역 안에서의 y의 평균 입니다.
- 분류 score
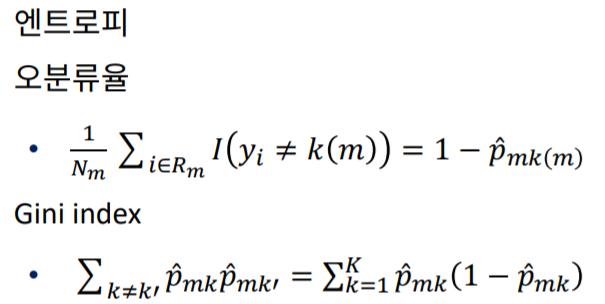
분류가 얼마나 잘 되었는지를 나타내는 지표들 입니다.
Decision tree의 depth가 깊어질 수록 위 지표가 점점 낮아지게 됩니다.
4. 정리
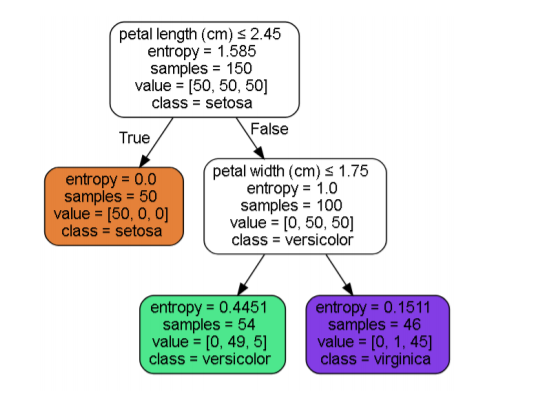
위 그림은 Classification tree를 도식화 한 것 입니다.
entropy는 내려갈 수록 점점 낮아지는 것을 확인 할 수 있으며 샘플또한 점점 분류가 되는 것이 보입니다.
-
이처럼 Decision tree의 장점은 해석력이 높고 직관적입니다.
-
하지만 변동성, 즉 데이터가 변함에 따라 학습모델이 쉽게 변하기 때문에 샘플에 매우 민감합니다.
마치며
이번 포스팅에서는 Decision tree에 대해 알아보았습니다. Classification tree, Regression tree를 동시에 알아보았으나 기본 개념이 간단하여 쉽게 이해 할 수 있을 것이라 생각합니다. Decision tree의 경우 depth를 너무 깊게하면 overfitting의 위험이 있기 때문에 random forest와 같은 이를 보안하는 방법이 있으나 이는 나중에 다른 포스팅에서 알아보려고 합니다.
