Support Vector Machine
1. SVM이란?
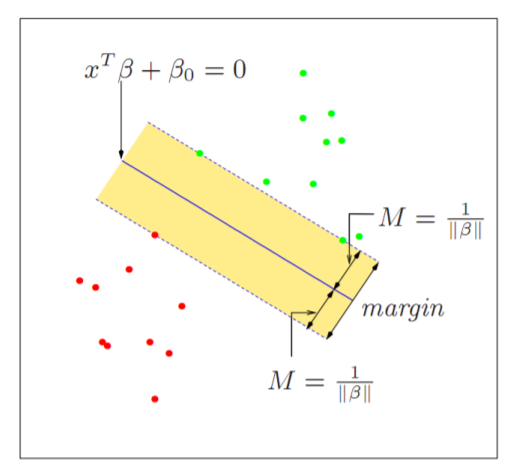
SVM이란 위와 같은
Decision boundary와Margin을 설정하여 데이터를 분류하는Classifier입니다.
두개의 그룹을 구분하는 Decision boundary는 수도 없이 많이 그릴 수 있으나 SVM은 Margin을 최대화 하는 Decision boundary를 찾는 것이 목표입니다.
이 때 가장 큰 Margin을 가질 수 있게 하는 데이터(점)을
Support Vector라고 부릅니다.
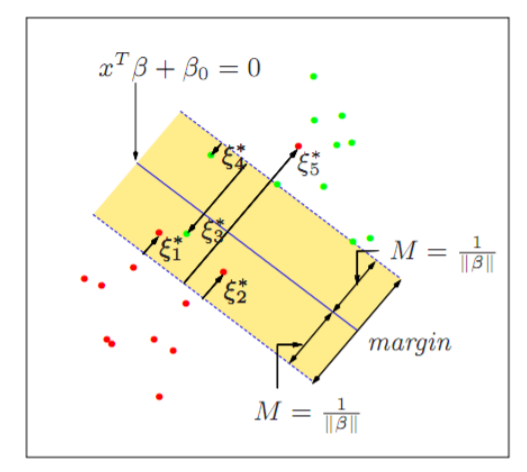
하지만 모든 SVM학습이 정확하게 구분 되는 것은 아니며 이는 특정 범위의 오차를 허용하는 것으로 해결 할 수 있습니다.
- SVR
SVM은 기본적으로
Classifier이지만 Y가 연속형 변수일 경우 또한 계산 할 수 있습니다.
이것을
SVR(Support Vector Regressor)라고 부릅니다.
2. SVM 모델
- Decision Rule

Decision Boundary를 위와 같이 정의합니다.
$||\beta||$는 절대값, 즉 모든 $\beta$의 크기의 합을 의미하며 정해주지 않는다면 상수배 만큼의 $\beta$가 존재하기 때문입니다.
이 boundary를 기준으로 우리는 Y를 판단 할 수 있으며 Decision Rule은 아래와 같습니다.
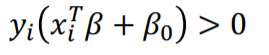
- SVM정의
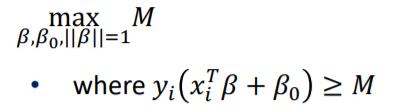
위 식은 Decision Rule에서 Margin을 고려한 값 입니다.
SVM의 목표는 이 M을 최대로 하는 $\beta$를 찾는 것 입니다.
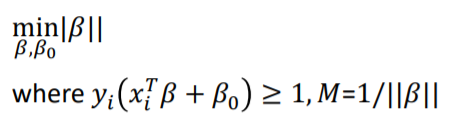
첫 Decision rule 설명파트에서 $||\beta||$를 1로 정하였으나 이번에는 $1/M$로 정의하여 정리한 것 입니다.
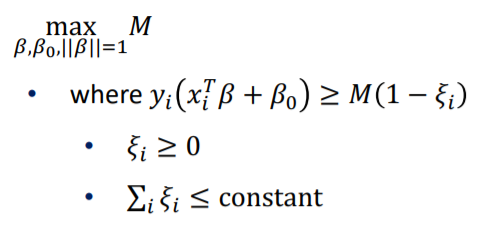
이번에는 에러를 허용하여 Decision rule을 적용시켜 본 것 입니다.
error는 Margin에서의 거리이며 error의 합을 constant로 정의 한 이유는 최대 오차 혀용범위를 지정하기 위해서 입니다.
때문에 이 constant는 직접 지정해 주어야 하며 나중에 C라는 상수로 표현됩니다.
이 C가 클수록 더 많은 error를 수용하는 것 입니다.
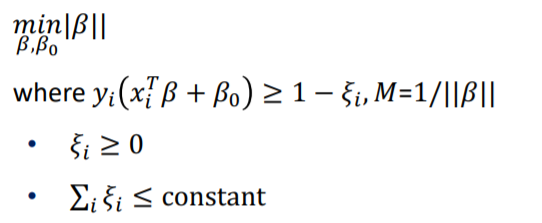
다시 한번 $||\beta||$를 지정하여 정리한 것 입니다.
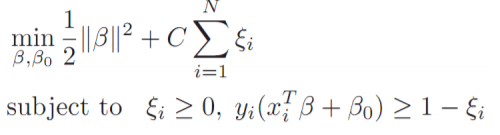
이를 cost function으로 정리하면 위와 같이 정리 할 수 있습니다.
이제 SVM의 목표는 C를 포함한 위 식을 최소화 하는 것 입니다.
- Lagrange Multiplier
위의 cost function을 최소화 하는 작업은 조건이 붙어있기 때문에 계산하기 쉽지 않습니다.
그렇기 때문에 특정 조건하에서 극값을 구하기 위해서
Lagrange Multiplier를 사용합니다.
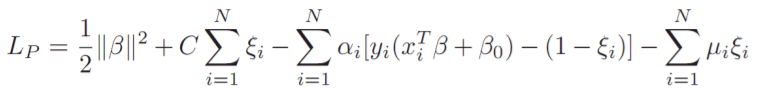
Lagrange Multiplier인 $\alpha$ 와 $\mu$를 도입한 Lagrange fucntion입니다.
이제 위 Lagrange function을 최소화 하는 $\beta$, $\beta$ 0, $\xi$i를 구하는 것 입니다.
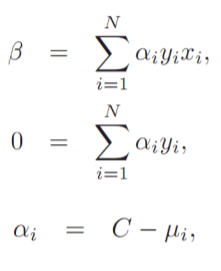
때문에 $\beta$, $\beta$ 0, $\xi$i 로 각각 편미분을 한 결과, 위와 같은 결과를 얻을 수 있으며 이를 정리하면 아래와 같은 새로운 Lagrange function을 얻을 수 있습니다.
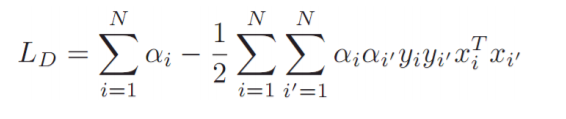
위의 Lagrange function을 최소화 시키는 $\hat \alpha$을 구할 수 있으며 이를 대입한다면 $\hat \beta$를 구할 수 있습니다.
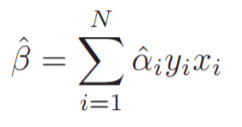
- Kurush-Kuhn-Tucker condition
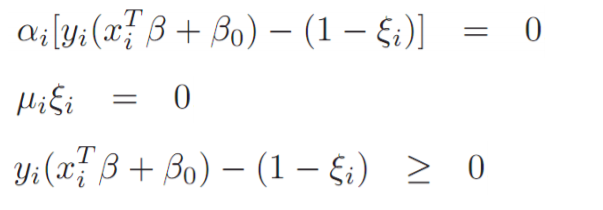
Kurush-Kuhn-Tucker condition에 의하면 위와 같은 조건을 만족 할 경우 L은 최적의 성능, 즉 Global minimum을 보장합니다.
Global minimum이란 4차식 이상일 경우 미분하여 구하는 최솟값이 두개 이상이게 되는데 이 중의 최솟값을 의미합니다.
- KKT condition 의미
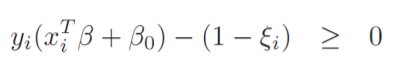
SVM상 정의를 만족하는 부분입니다.
error보정을 완료한 후 margin의 위 혹은 바깥쪽에 데이터가 존재함을 의미합니다.
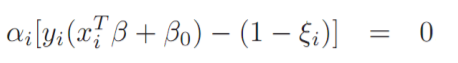
위의 식이 0이 되는 경우는 $\alpha$가 0인경우, SVM정의를 만족하는 부분이 0이 되는 경우 입니다.
$\alpha$가 0이 되는 경우, 즉 데이터가 Margin 범위의 바깥에 있는경우는 $\hat \beta$ 또한 마찬가지로 0이므로 $\beta$를 구하지 않습니다.
SVM정의를 만족하는 부분이 0이 되는 경우는 데이터가 정확히 Margin 위에 위치 할 때 입니다.
이 경우 $\alpha$는 0이 아니게 되며 우리는 $\hat \beta$를 구할 수 있습니다.
이 경우의 데이터, 즉 i를 우리는
Support Vector라고 합니다.
3. 심화
- Kernel SVM
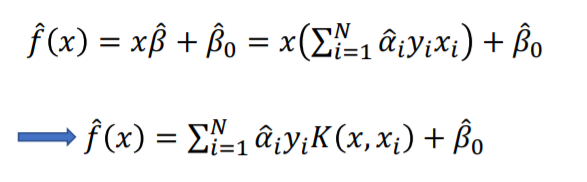
SVM과 유사하지만 x에 Kernel을 집어 넣습니다.
즉 x와 $\hat \beta$간의 선형관계를 깨고 비선형, Kernel을 도입한 것 입니다.
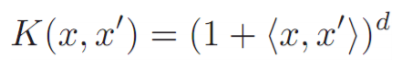
d를 올려줌에 따라 복잡도를 더해 줄 수 있습니다.
하지만 너무 많이 올린다면 overfitting의 위험이 있습니다.
<x,x’>은 내적을 의미합니다.
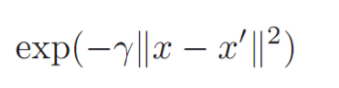
이 외에도 가우시안 커널과 같이 다양한 커널을 선택 할 수 있습니다.
- One Class SVM
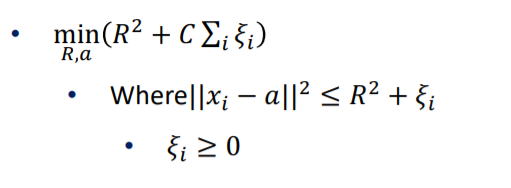
One class SVM은 비 지도학습, 그 중 군집학습 입니다.
즉 종속변수 Y가 존재 하지 않으며 데이터들을 하나의 그룹으로 만드는 학습 입니다.
One class SVM은 M 대신 R이라는 반지름을 사용하며 중심위치를 a라고 할 경우 위의 식을 최소화 하는 SVM학습 방법입니다.
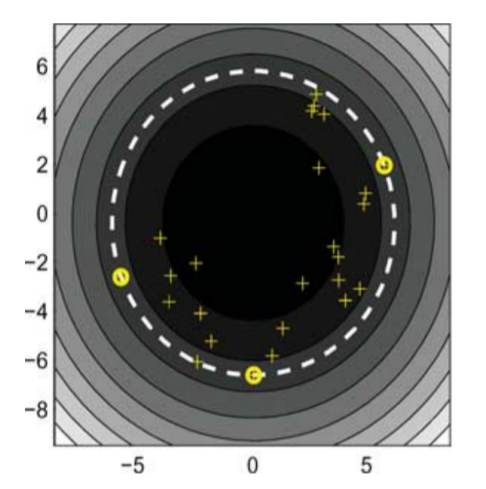
결과 위와 같이 나오며 노란색 원 으로 표현 된 점은 Support Vector, 흰 점선이 Boundary입니다.
- SVR
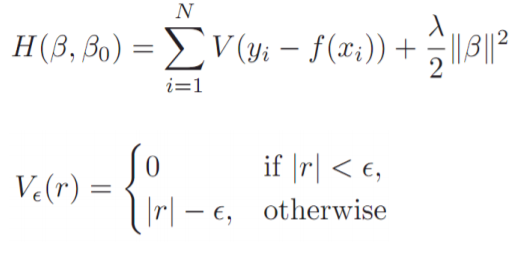
SVR은 SVM의 모델을 바탕으로 학습하는 Regression 모델 입니다.
위의 함수를 최소화 하는 것을 목표로 하며 SVM과 다르게 Margin 바깥쪽의 데이터를 고려하여 계산합니다.
r은 margin 바깥쪽의 데이터 중 Decision boundary와의 거리이며 $\epsilon$은 margin을 의미합니다.
이 때 SVM과 마찬가지로 x대신 Kernel을 적용하여 선형모델에서 비선형 모델로 계산 할 수 있습니다.
4. SVM의 장단점
장점
-
SVM은 LDA와 다르게 데이터 간의 공분산 구조를 반영 할 필요가 없습니다. 때문에 데이터의 분포를 가정하기 힘들 경우 사용 할 수 있습니다.
-
또한 boundary근처의 관측치만 고려 할 수 있습니다.
-
결정적으로 예측의 정확도가 높습니다.
단점
-
하지만 C를 결정해 주어야 합니다.
-
또한 모형 구축에 시간이 오래걸린다는 단점이 존재합니다.
마치며
이번 포스팅에선 SVM에 대하여 알아보았습니다. SVM은 수학적 역사가 무척 깊은 기술로 자세히 공부하자면 굉장히 많은 양을 다루게 됩니다. 하지만 정작 중요한 것은 SVM이 어떤 원리로 작동하는가, 어떤 장점, 단점이 있는가 정도라고 생각합니다.
