Linear Discriminant Analysis
1. LDA란
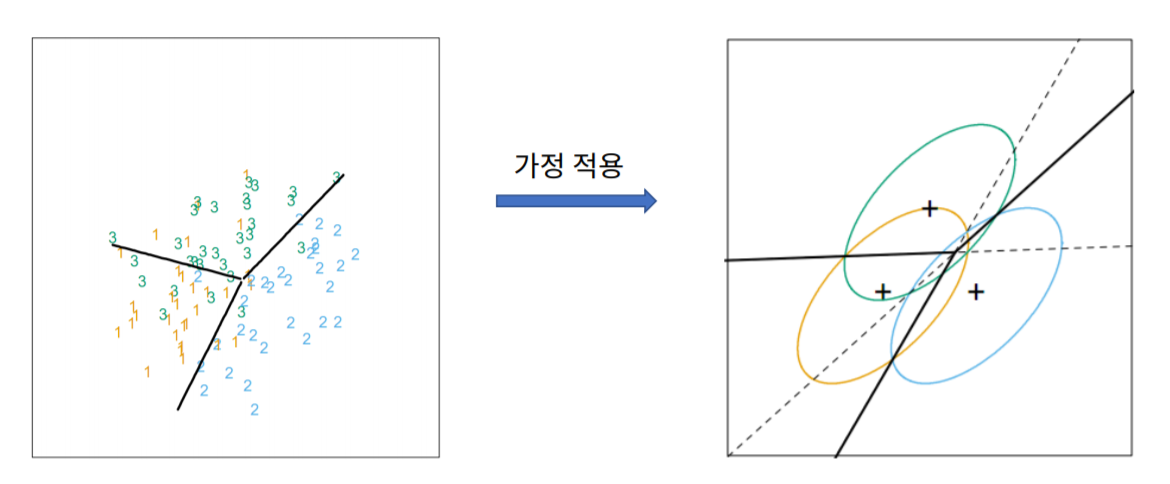
먼저 LDA는 두가지 가정이 존재합니다.
첫번째, 각 집단은 정규분포 형태의 확률분포를 가진다.
두번째, 각 집단의 공분산은 서로 비슷한 형태의 구조를 가진다.
이러한 가정하에 Discriminant function을 생성하여 분류(classification)하는 모델입니다.
- Discriminant function

LDH는 Discriminant function이라는 위와 같은 식을 가지고 있습니다.
Discriminant function은 데이터가 특정 그룹, 위 그림에서는 k 그룹에 존재할 확률입니다.
즉 LDH는 이 discriminant function이 최대가 되는 그룹을 찾아 분류(Clssify)하는 모델입니다.
이 식을 이해하기 위해서는 아래 설명할 두가지 수학적 개념을 이해하여야 합니다.
2. 다변량 정규분포
- 정규분포
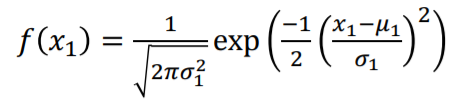
- 이변량 정규분포
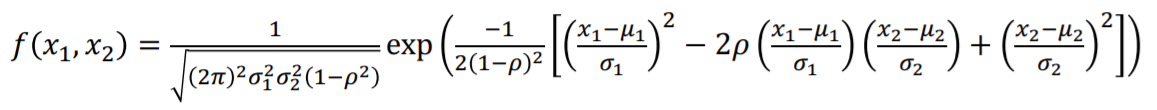
- 다변량 정규분포
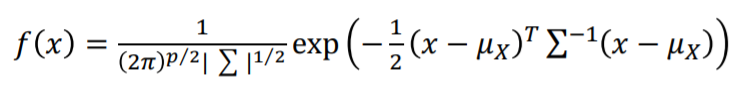
p는 그룹의 갯수입니다, 또한 시그마는 공분산 행렬입니다.
LDH는 모든 그룹이 정규분포를 따른다고 가정하니 전체 분포는 다변량 정규분포로 표현할 수 있습니다.
LDH에는 두개 이상의 그룹이 존재할테지만 한개의 decision boundary를 그리기 위해서는 우선 두개의 그룹을 뽑아 순차적으로 비교해야 합니다.
이때 선발된 그룹을 k,l 그룹이라고 칭하겠습니다.
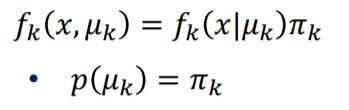
우선 p개의 그룹에서 k그룹의 변수가 나올 확률을 $\pi k$ , 사전확률 이라고 합니다. 그렇다면 다변량 정규분포에서 k 그룹이 나올 확률은 확률분포함수에 $\pi$를 곱한 값이 될 것 입니다.
그렇다면 이러한 확률식을 간단히 계산하기 위해 사전확률을 고려해서 로그를 취한 k그룹과 l그룹을 비교하면 다음과 같이 식이 형성됩니다.
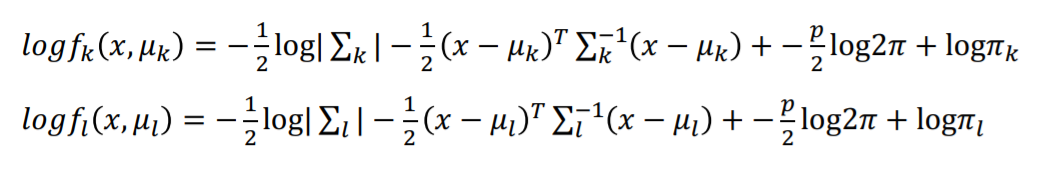
LDH에서는 그룹들의 공분산 구조가 서로 비슷하다고 가정합니다. 그렇기에 $\sum$k와 $\sum$l은 서로 같다고 가정하는 것과 같습니다. 즉 $\sum$ k$ = \sum$ l$ = \sum$ 입니다.
이 때 그룹변수인 k혹은 l과 관련이 없는 부분을 모두 상수 C라고 정의하고 정리한다면 아래와 같은 discriminant function을 얻을 수 있습니다.
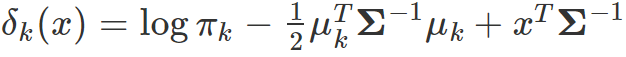
이 discriminant function은 다변량 정규분포에서 특정 그룹의 확률분포 함수입니다.
LDH 가 Y를 추정하는 방법은 이 discriminant function이 가장 커지는 그룹을 찾는 것 입니다.
그렇기 때문에 특정 두 그룹의 활률분포그룹이 같아지는 지점, 즉 특정 데이터 x가 k그룹일 확률과 l그룹일 확률일 같아지는 지점이 decision boundary입니다.
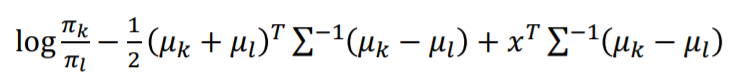
3. Projection(사영)
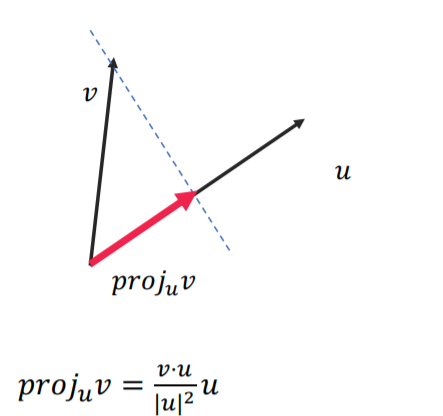
Projection의 정의는 위와 같습니다.
특정 벡터를 특정 축에 수직선을 내려 그 크기와 방향을 나타내는 것이며 만약 u가 크기가 1인 방향벡터라면 projection의 값은 두 벡터의 내적과 같습니다.
- Decision boundary
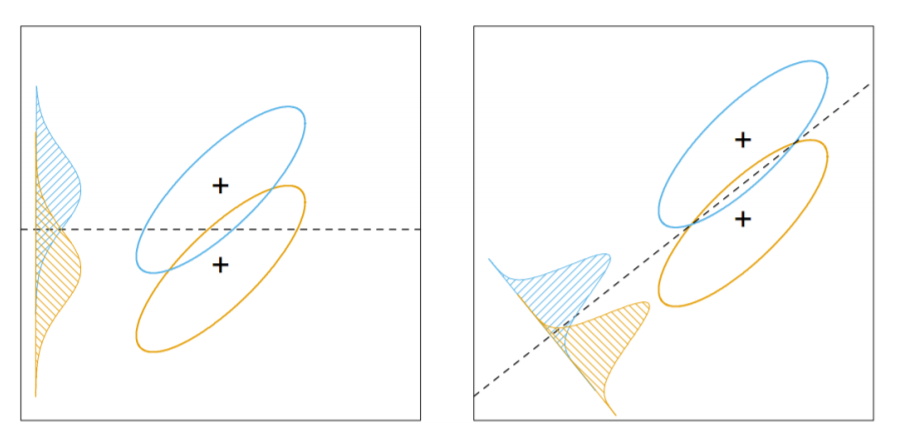
decision boundary는 두 그룹을 나누는 기준 벡터 입니다.
decision boundary를 정하기 위해서는 평균의 차를 최대화 하는 방향으로 설정 해야 확실하게 두 그룹을 구분 할 수 있습니다.
그렇지만 첫번째 그림처럼 무작정 평균의 차를 최대화 시킨다면 두 그룹의 분산이 너무 크기 때문에 제대로 된 분류를 할 수 없을 가능성이 큽니다.
그렇기 때문에 LDA의 decision boundary는 오른쪽 그림과 같이 분산대비 평균의 차이가 극대화 하는 boundary를 찾아야 합니다.
- Projection을 이용하여 Decision boundary찾기
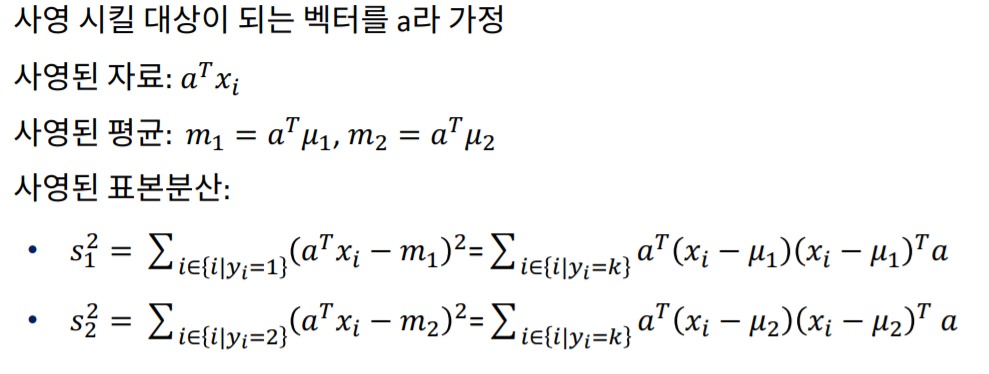
LDA의 decision boundary는 평균의 차를 최대화 하면서 분산을 최소화 하는 지점 입니다.
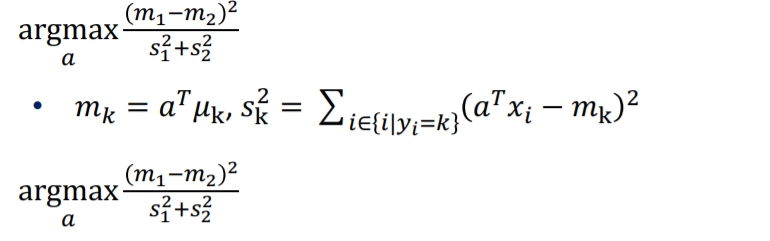
위 식은 아래로도 표현이 가능합니다.
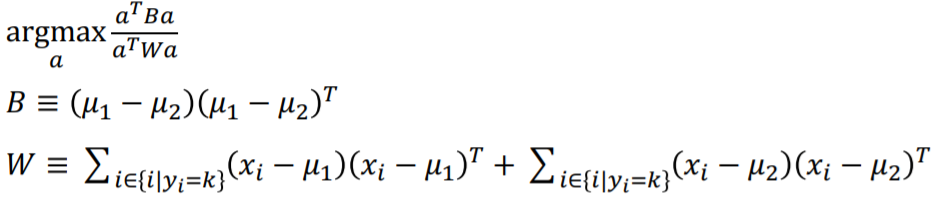
이제 위 식의 최댓값을 구하기 위해 미분해 본다면 아래와 같은 eigen vector형태로 구할 수 있습니다.
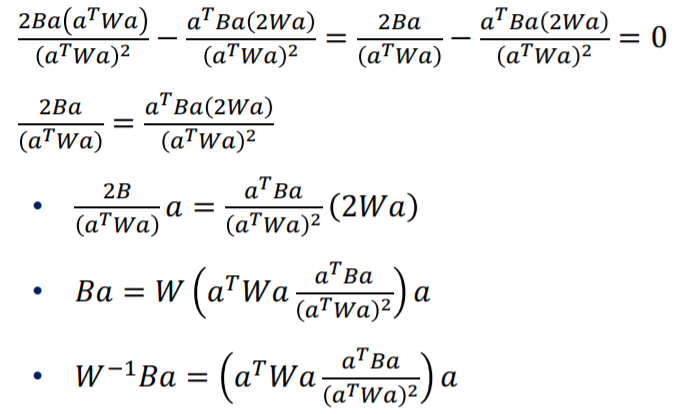
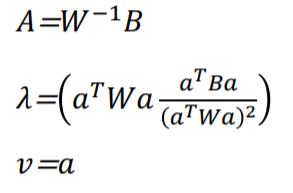
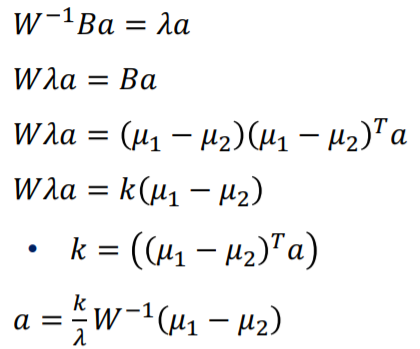
이때 벡터의 길이를 무시하고 방향만 본다면 아래와 같습니다.
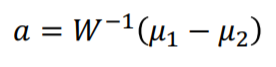
W는 error의 제곱의 합, 즉 공분산을 뜻합니다. 또한 $\sum$ 은 공분산 행렬이기 때문에 각각의 분산을 무시한다면 서로 대체할 수 있으며 대체한다면 다변량 정규분포에서 구한 식과 같은 역할을 하게 됩니다.
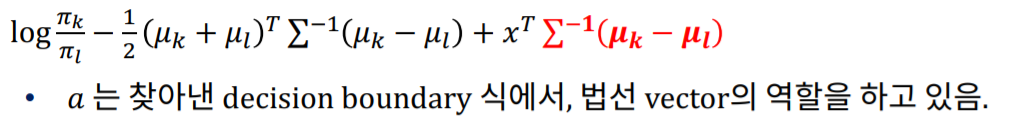
4. LDA

수학적 개념을 이해 한 후 다시한번 LDA의 discriminant function을 확인해 보겠습니다.
LDA는 이 discriminant function이 최대가 되는 $\hat y$을 추정하는 방식입니다.
LDA는 naive classifier와는 다르게 자료들 간의 공분산구조, 즉 상관관계가 있어도 추정할 수 있는 장점이 있습니다.
하지만 데이터가 정규분포를 따진다는 가정과 공분산 구조가 같다는 가정을 하기 때문에 이 가정에 위배되는 경우 모델이 잘 작동하지 않습니다.
- QDA

공분산 구조가 같다는 가정을 제거한 LDA가 QDA입니다.
LDA는 공분산 구조, 즉 $\sum$ 이 다 같다고 가정하기 때문에 일차식 형태(Linear)하지만 QDA는 각 그룹별 공분산 구조가 다르기 때문에 이차식(Quadratic)형태로 존재합니다.
LDA는 decision boundary 가 직선으로 구성되어 있지만 QDA는 곡선 boundary가 가능합니다.
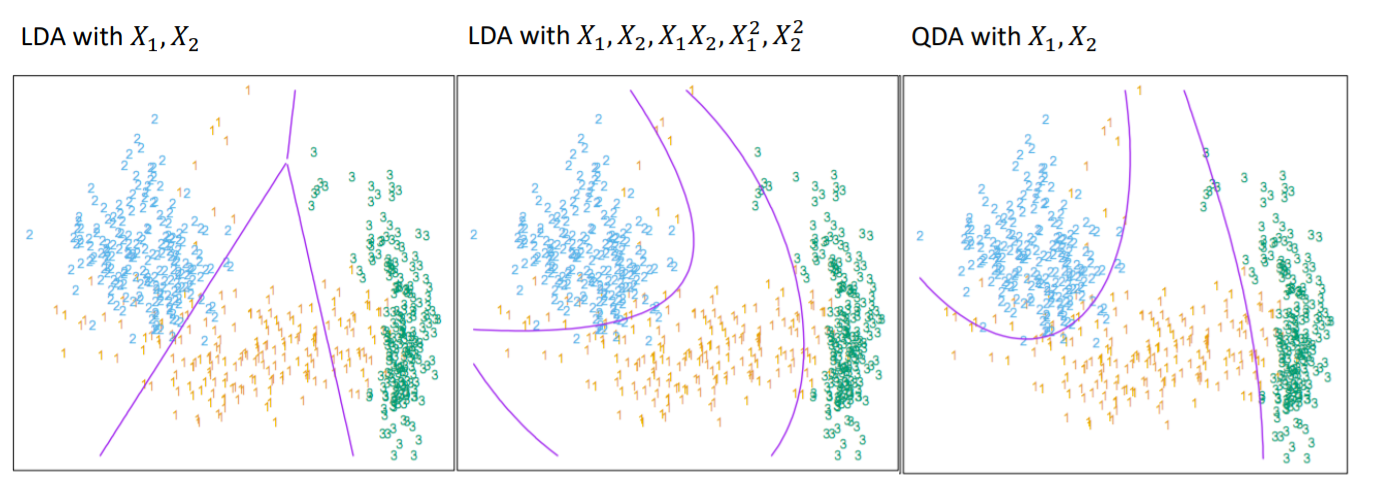
QDA는 공분산 구조가 다를 경우도 추정이 가능합니다.
하지만 설명변수의 갯수, 그룹의 갯수가 많을경우 많은 데이터를 필요로 하는 단점도 존재합니다.
마치며
이번 포스팅은 LDA에 관하여 알아보았습니다. PCA와 마찬가지로 기존의 차원을 새로운 차원으로 Projection하여 계산한다는 비슷한 면이 존재합니다. LDA는 새로운 차원에서의 분포를 이용한 분류방법이기 때문입니다.
