PCA
1. PCA의 필요성
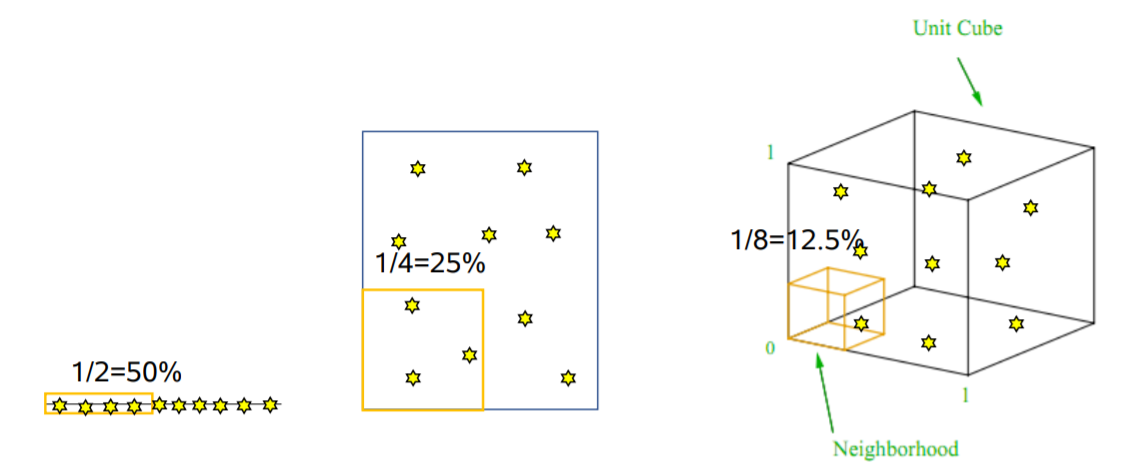
차원이 커질수록 한정된 자료는 커진 차원의 패턴을 잘 설명하지 못합니다.
또한 쓸데없는 변수, 즉 변수들 사이의 상관관계가 매우 크거나 예측하고자 하는 변수와 관련이 없는 변수는 모델에 악영향을 끼칩니다.
그러나 상관관계가 크다고 해서 분석에서 제외해 버린다면 그만큼 정보의 손실이 발생하게 됩니다. 그렇기 때문에 차원을 줄이면서 정보의 손실을 최소화 하기 위하여 Principal Component Analysis를 활용합니다.
2. PCA의 개념
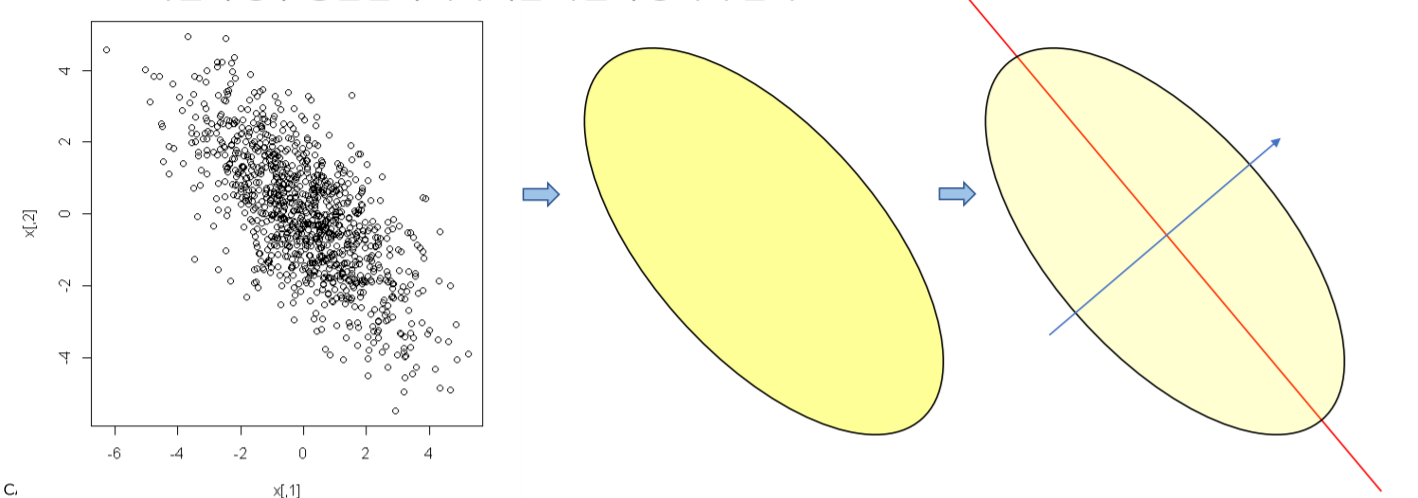
PC(Principal Component)를 얻어 낸다는 것은 공분산이 데이터의 형태를 변형시키는 방향의 축과 그것과 수직인 새로운 좌표축을 찾는 과정입니다.
위 그림의 2차원 데이터의 경우 두개의 X의 공분산이 타원형태로 이루어져 있으며, 이것의 장축(빨강선)과 단축(파란선)을 찾아내는 과정입니다.
- PC score
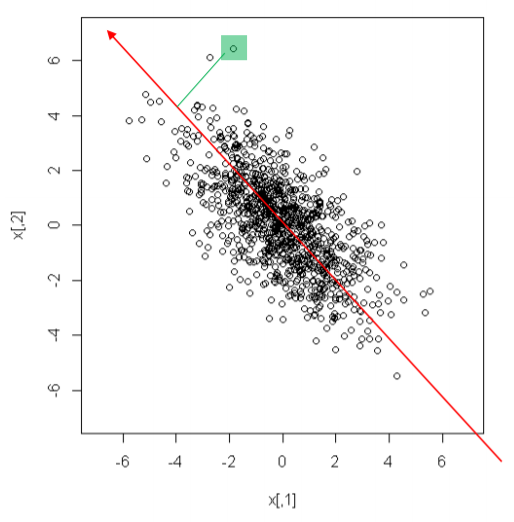
PC score는 새롭게 찾아낸 좌표축에서의 좌표값을 의미합니다.
위 그림에서는 새롭게 찾아낸 빨간 대각선 축을 기준으로 수직으로 내린 위치를 뜻합니다.
3. Eigen vector
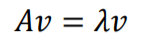
정방행렬 A에 대하여 $\lambda$(eigen value)라는 스칼라 값과 $\nu$(eigen vector)라는 벡터로 표현하는 방식 입니다.
즉 A(PxP)라는 행렬을 $\nu$라는 방향벡터와 $\lambda$라는 크기의 스칼라의 곱으로 표현하는 것을 뜻합니다.
4. SVD(Singular-Vector Decomposition)

간략히 설명하면 X라는 행렬을 U, D, V라는 행렬로 분해하여 표현하는 것을 의미합니다.
여기서 U와 V는 orthogonal matrix 즉 V’V = I 로 표현되는 행렬입니다. 또한 D는 diagonal matrix, 대각선에만 요소가 들어있는 행렬입니다.
SVD를 사용하는 이유는 공분산 행렬의 eigen vector 와 eigen value를 편하게 얻기 위함입니다.

eigen vector를 찾는 법을 간단하게 설명하고자 합니다.
행렬 X를 제곱, 즉 X’X를 해준 뒤 V를 양 항의 오른쪽 끝에 곱해준다면 쉽게 eigen vector의 형태를 얻을 수 있습니다.
위와 같은 과정 때문에 SVD로 형태를 변형시켜 준다면 V가 eigen vector, $D^2$를 eigen value라고 쉽게 얻을 수 있습니다.
5. PCA수행 과정
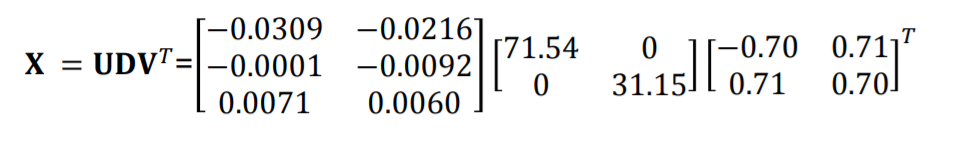
X1과 X2로 구성된 1000개의 관측치를 mean centering, 평균을 0으로 맞춰준 후 SVD를 수행한 식이 위와 같습니다.
SVD과정은 컴퓨터가 정해진 연산에 따라 자동으로 계산해 줍니다.
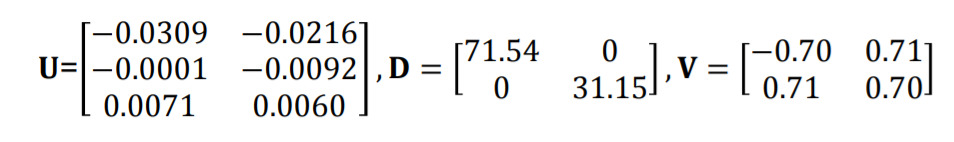
즉 eigen vector V와 eigen value D는 다음과 같습니다.
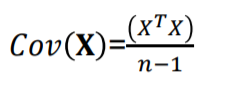
mean centering된 X에 관하여 공분산 cor(X)를 구하는 방법은 위와 같습니다.
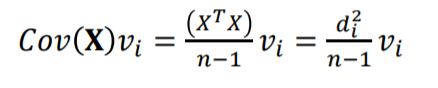
따라서 쉽게 공분산의 eigen vector와 eigen value를 얻어 낼 수 있으며 그 값은 아래와 같습니다.
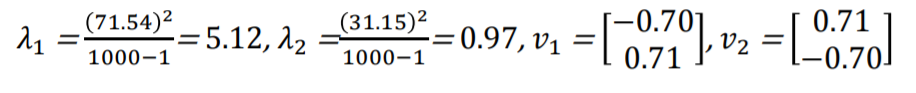
- PC score
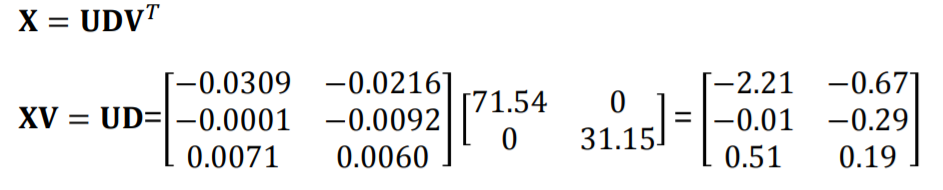
이렇게 구해진 XV값이 PC score입니다. 즉 새롭게 축소된 eigen vector라는 차원 안의 value이며 이를 분석에 활용하게 됩니다.
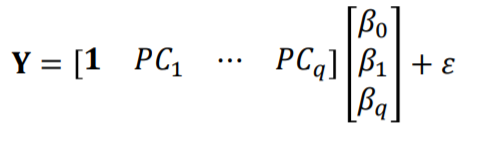
이때 PC score를 큰 순서대로 내림차순 하여 PC1 부터 PCq까지 나열하여 사용합니다.
- PC score의 기하학적 해석


v는 eigen vector로서 새롭게 축소되어 창조된 차원(빨간색 좌표축) 입니다.
PC score는 이때 관측치와 eigen vector의 내적, 즉 수직으로 내렸을 때 의 크기이므로 v라는 좌표안에서 크기입니다.
즉 PC score로만 구성된 새로운 DATA SET을 얻게된 것 이며 공분산을 활용하였기 때문에 상관관계가 존재하는 입력변수들을 축소 시킴과 동시에 상관관계가 존재하지 않는 부분만 PC score라는 형태로 얻게 된 것 입니다.
6. Kernel PCA
- Kernel PCA
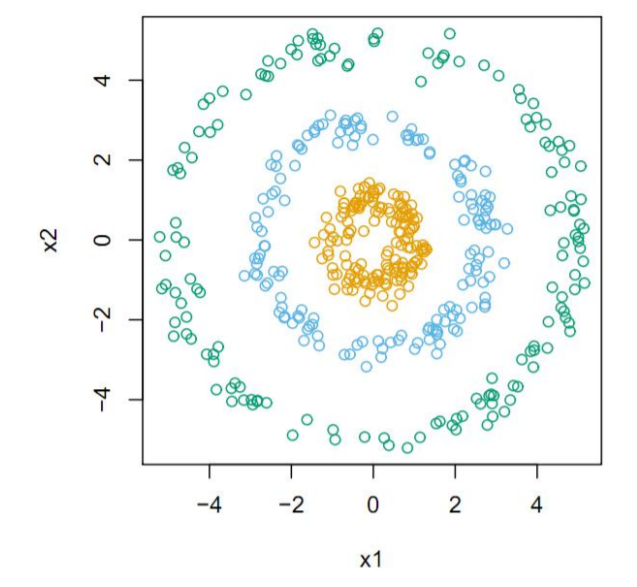
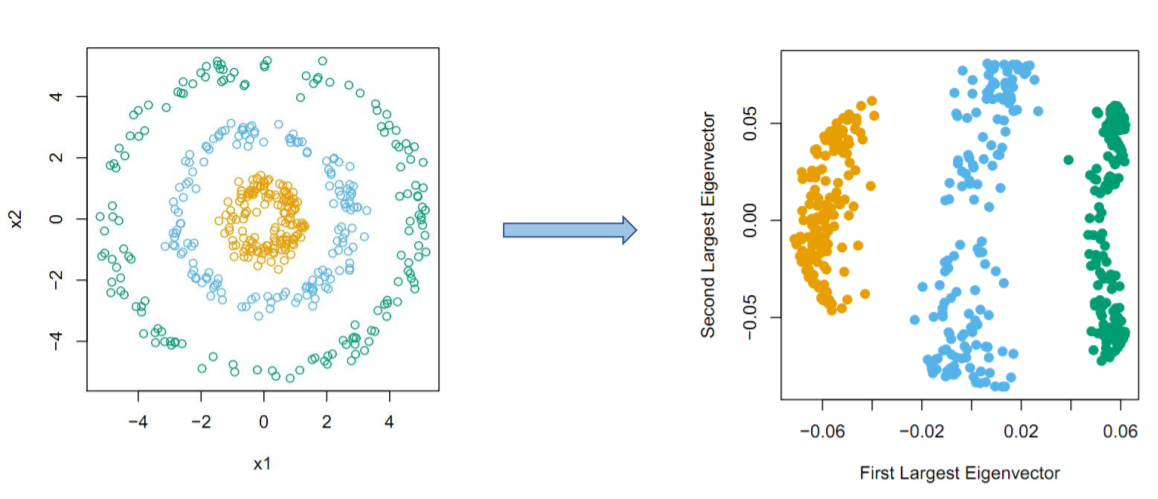
Kernel PCA의 경우 위 그림과 같이 비 선형적인 관계에서 사용합니다.
위 그림의 경우 공분산은 0일 것 이며 이는 PCA를 사용 하지 못함을 의미합니다.
- Kernel Matrix
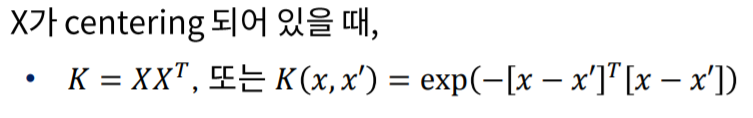
K를
Kernel Matrix라고 하며 이는 관측치 사이의 유사도 입니다.
즉 두개의 관측치의 거리, 혹은 유사도가 비슷할 시 값이 커지며 멀어질수록 값이 작아지게 됩니다.
위 식의 K는 자주쓰이는 Kernel Matrix의 예시 중 두가지 이며 첫번째 식의 경우 X끼리의 공분산 X’X 을 Transpose한 관계에 있습니다.
즉 변수들 사이의 공분산을 Transpose한 결과 관측치 사이의 유사도가 되었다는 개념입니다.
- PC score

- 결과
마치며
이번 포스팅에서는 PCA, 차원축소에 대해 알아보았습니다. 상당히 어려운 개념이나 왜 PCA가 필요한지, 어떠한 과정을 거치는지, 결과가 어떻게 나오는지 에 집중하면 이해하기 편할 것 이라 생각합니다.
