회귀계수 축소법
1. 회귀계수 축소란?
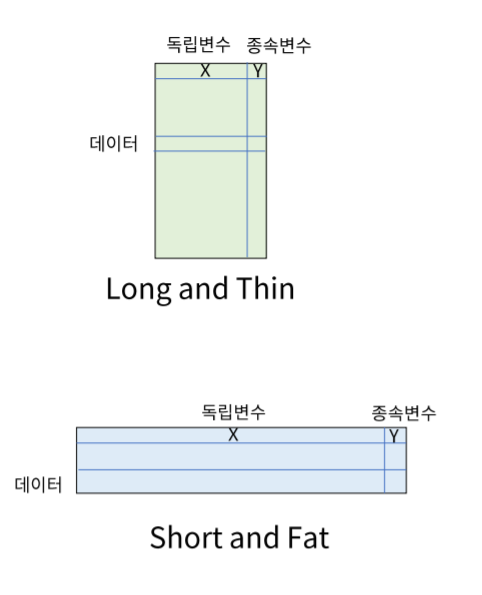
- 분석용 데이터는 X, 입력변수 사이에 상관관계가 적은 것이 이상적입니다.
- 또한 X 와 Y의 상관관계는 커야하며 많은 양질의 데이터가 있는 Long and Thin형태가 가장 이상적입니다.
- 하지만 대부분의 데이터는 이와 반대로 Short and Fat형태를 지니고 있으며 별로 중요하지 않은 변수가 많다면 분석의 성능을 저하시킵니다.
- 그렇기에 변수선택(Variable Selection) 을 하게 되며 그 방법이 계수축소법 입니다.
2. 계수축소법
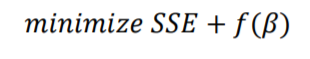
계수 축소법은 3가지 Ridge, Lasso, Elastic-Net 가 있습니다.
하지만 공통적으로 SSE + $f(\beta)$, 즉 SSE와 회귀계수를 최소화 하는 방법을 사용합니다.
- Ridge

Ridge는 회귀계수를 제곱하여 합한 값을 SSE와 더하여 최소화 합니다.
$\lambda$는 직접 선택해야 하는 변수이며 $\lambda$에 따른 회귀계수들의 변화는 아래와 같습니다.
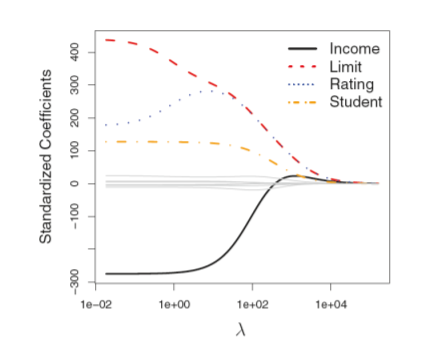
단 Ridge는 회귀계수를 0으로 만들지 않으며 단지 0에 가깝게 만듭니다.
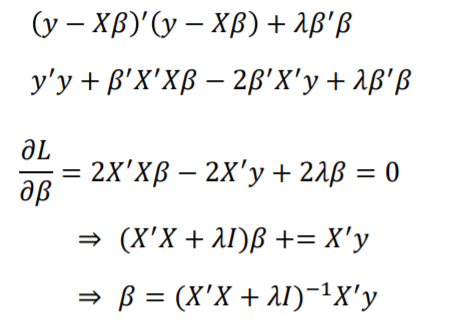
X, 즉 입력변수들 사이에 강한 상관관계가 있다면 다중공선성이 발생하며 X’X의 역행렬을 구할 수 없습니다.
계수축소법은 강제로 $\lambda$$I$라는 값을 추가하여 역행렬을 구할 수 있게 한 형태입니다.
- Lasso
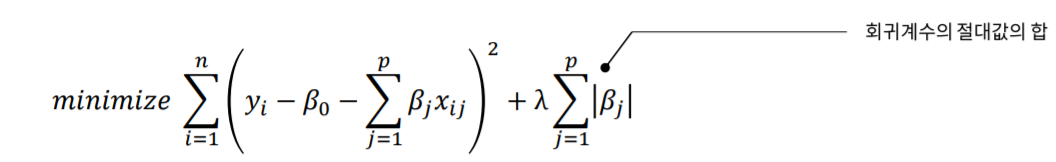
Ridge가 회귀계수를 제곱하여 합하였다면 Lasso는 절대값의 합 입니다.
그렇기 때문에 Ridge가 회귀계수를 0으로 만들지 않았다면 Lasso는 $\lambda$가 커질 시 회귀계수를 0으로 만듭니다.
이외에 Ridge와 큰 차이점은 없으며 Lasso의 회기계수는 Ridge와 다르게 한번에 구할 수 없습니다.
- Elastic-Net
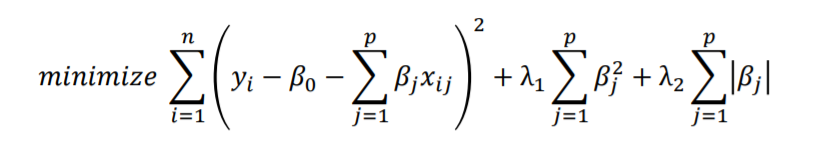
Ridge와 Lasso의 비율을 적절하게 섞은 것 입니다.
Ridge의 장점과 Lasso의 장점을 절절한 비율로 섞어 사용할 수 있으며 상황에 따라 세가지 방법중 가장 적절하다고 생각하는 방법을 사용하면 됩니다.
- **$\lambda$의 설정

좌측이 Ridge, 우측이 Lasso입니다.
$\lambda$의 값을 변화시켜가며 MSE가 최소인 경우를 찾으면 됩니다.
3. 정리
- 계수축소법은 입력변수들 간의 상관관계를 최소화 시키기 위해 사용하는 방법입니다.
- 상관관계가 큰 변수들은 $\lambda$에 따라 회귀계수가 크게 줄어들 것 이며 이를 Lasso를 이용하여 0으로 만들어 삭제하는 방법, 혹은 강한 상관관계 속에 상관 관계를 가지지 않는 부분을 최대한 활용하기 위하여 Ridge를 사용하는 것은 분석가의 판단 입니다.
마치며
이번 포스팅에서는 계수축소법, 즉 변수를 선택하는 방법에 대해 알아보았습니다. 다음 포스팅은 계수를 축소하는 것이 아닌 차원, 즉 변수의 갯수를 조정하는 방법에 대해 알아보려고 합니다.
