로지스틱 회귀

1. 로지스틱 회귀(Logistic Regression) 란?

• 두개의 카테고리, 즉 0 과 1 binary형태의 출력변수를 예측하는 회귀분석 방법 입니다.
• 회귀(Regression)이지만 분류(classification) 지도학습 입니다.

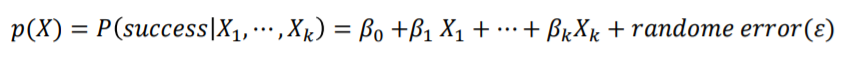
• 로지스틱 회귀에서는 k개의 입력변수를 사용하여 성공, 실패 확률을 예측하기 위한 성공확률 $p(x)$를 모델링 합니다.

• 이때 왼쪽, 즉 $p(x)$는 확률이기 때문에 [0, 1] 의 범위를 가지지만 오른쪽, 선형 회귀함수로 표현된 우항은 [-∞, ∞]의 범위를 가지기 때문에 형태를 조금 변형 해 주어야 합니다.

• 로지스틱 함수(Logistic Function)

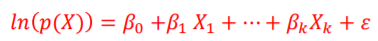
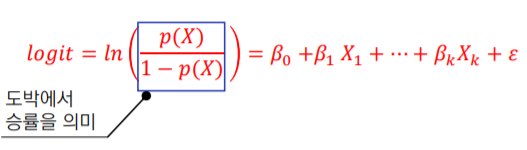
범위의 차이를 없애기 위해 왼쪽에 로그를 취합니다. 하지만 로그를 취하면 -∞는 만족하지만 최댓값이 ∞ 을 가지지 못하기 때문에 다시한번 보정하여 logit이라는 변수를 만들게 됩니다.

이렇게 logit 으로 부터 도출된 Y가 1일 확률 $p(X)$는 아래와 같습니다.

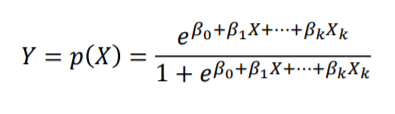
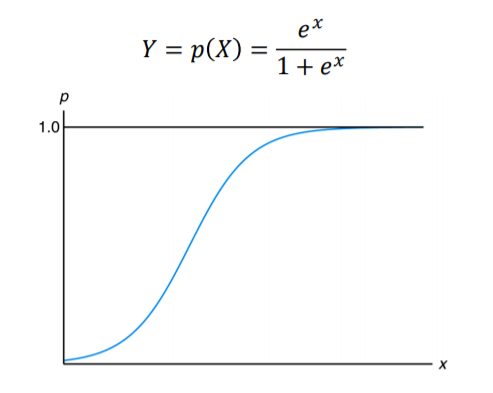
아래의 식은 exp부분을 간략하게 정리한 것이며 그래프는 입력변수가 1개일때, 즉 입력변수의 차원이 1일 때의 그래프입니다.

간단히 파악하자면 p(X)가 0.5, 즉 1이 나올 확률이 0.5 보다 크다면 출력 변수를 1로 출력하고 그렇지 않다면 0으로 구분하게 됩니다.

• 로지스틱 회귀계수

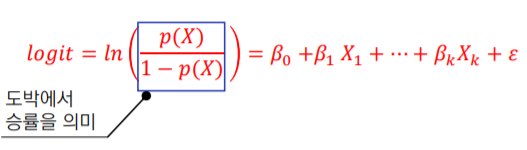
로지스틱 회귀에서의 회귀계수는 logit에서 확인 할 수 있습니다.

logit은 선형 회귀와 똑같은 형태를 가지고 있지만 이 계수를 구하는 방법은 선형 회귀와는 다릅니다.

SSE를 미분하여 0이 되는 계수를 찾는 것이 아닌, 최대우도법(maximum likelihood)방법을 사용합니다. 또한 이때의 분포는 베르누이 확률 분포를 사용합니다.

계산과정은 생략하겠습니다.

• 회귀계수의 의미

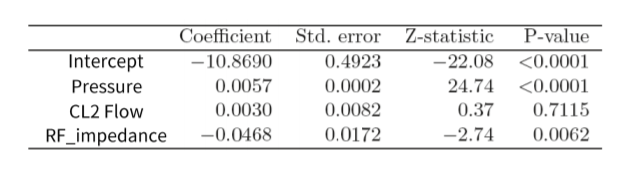
RF_impedance는 회귀계수 -0.0468를 가지고 있습니다. 이는 RF_impedance가 1단위 증가 할때 logit이 0.0468단위 감소한다는 의미 입니다.

이를 해석하는 방법은 logit으로 해석하는 방법과 odds로 해석하는 방법이 아래와 같이 존재합니다.

마치며

이번 포스팅에선 Logistic Regression에 대해 알아보았습니다. 중간에 회귀계수를 구하는 수식을 생략하였지만 이를 유도하는 과정보다는 그 결과와 의미를 파악하는 것이 우선이라고 생각하였기 때문입니다.