선형회귀 2
1. 다중공선성
- 다중공선성(Multicollinearity)
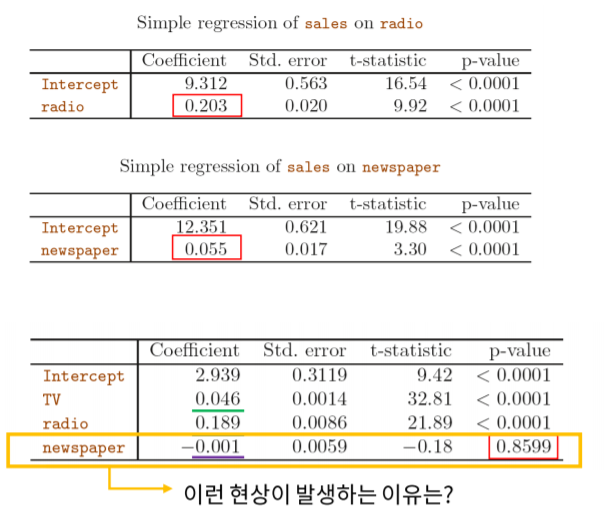
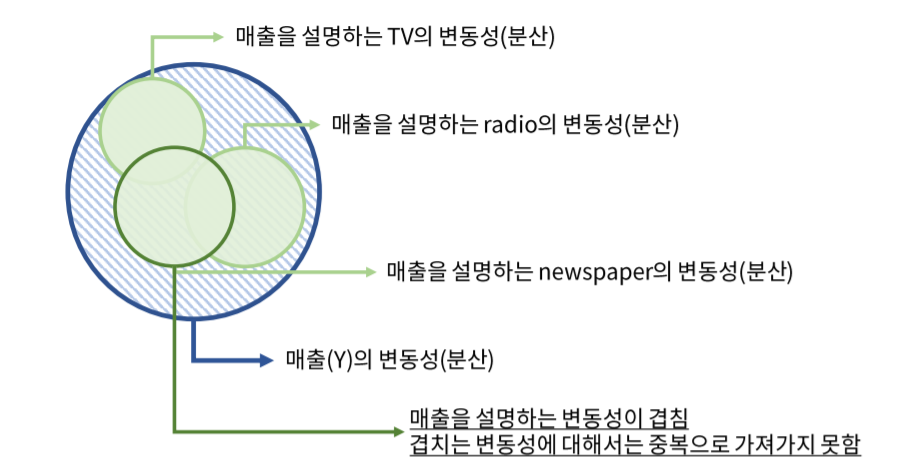
다중공선성은 변수들 간에 강한 선형관계에 있는 것을 뜻합니다.
위의 그림과 같이 newspaper는 매출을 설명하는 변동성이 TV와 Radio와 겹치게 됩니다. 때문에 회귀상수가 제대로 측정되지 않게 됩니다.
1.1 다중공선성의 진단
- VIF(Variance Inflation Factor)
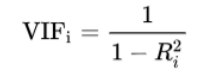
변수들 간의 Correlation을 진단하여 계산합니다.
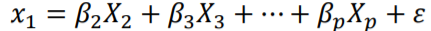
예를들어 X1의 VIF를 계산하기 위해서는 X1을 종속변수(Y), 나머지를 독립변수(X)로 하는 회귀모델을 만들고 이때 R squared값을 구합니다.
그렇게 구한 R squared를 VIF계산식에 넣어 VIF1을 구하면 1번 변수, X1 에 대한 다중공선성을 진단 할 수 있습니다.
일반적으로 VIF가 10을 넘어가면, 즉 R squared가 0.9 이상이면 다중공선성이 크기 때문에 의미가 없는 변수라고 판단합니다.
1.2 다중공선성을 해결하는 방법
-
가장 많이 사용하는 방법은 Features 수를 줄이는 것 입니다.
-
의미없는 값들이 늘어나면 자연스럽게 R squared값이 늘어나게 되므로 중요한 변수만 사용하는 것이 의미없는 변수를 다 밀어 넣은 것 보다 신뢰성이 높습니다.
-
이 외에도 PCA, Ridge, AutoEncoder등 다양한 기법이 있으나 현재까지도 큰 이슈로 남아있는 부분 입니다.
2. 회귀모델의 성능지표
- R squared
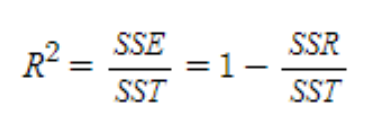
이미 한번 포스팅 한 적 있는 R squared입니다.
하지만 R squared는 변수가 증가하면 자연스럽게 증가하기 때문에 회귀분석의 성능지표로는 큰 의미가 없습니다.
- Adjusted R squared
$Adjusted R^2 = 1 - $$SSE/(n-p-1)\over SST/(n-1)$
R squared를 구성하는 SSE와 SST를 각각의 자유도로 나누어주고 1로 뺀 값입니다.
자유도를 구성하는 n은 총 입력변수(데이터)의 갯수이며 p는 features의 갯수 입니다.
- MSE(Mean Squared Error)
$MSE = $ $1\over n$ $\sum$ $(y- \hat y)^2$
간단하게 SSE를 n, 데이터의 갯수로 나눠준 값 입니다.
잔차의 평균이며, 회귀분석은 MSE를 최소화 하는 방향으로 설계 되나 너무 작아진다면 overfitting이 일어나게 됩니다.
- MAPE(Mean Absoulute Percentage Error)
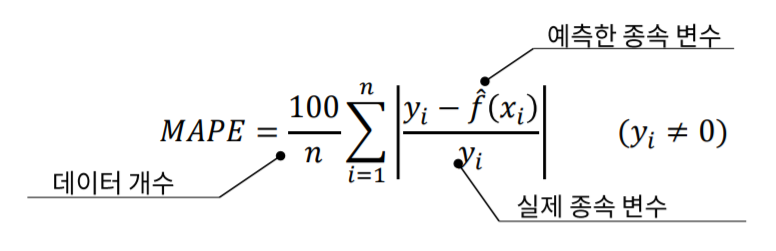
MSE는 잔차의 평균이기 때문에 얼마나 잔차가 심하게 나는지 알기 어렵습니다.
그래서 MAPE는 이를 %로 나타냅니다.
- AIC(Akaike Information Criterion)
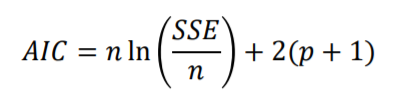
모델의 성능지표로서 MSE($SSE\over n$)에 features 수만큼 패널티를 주는 구조입니다.
n이 커지면 수치가 작아지고 p가 커지면 수치가 커지게 됩니다.
그렇기에 AIC는 낮을수록 더 좋은 모델이라는 수치입니다.
- BIC(Bayes Information Criterion)
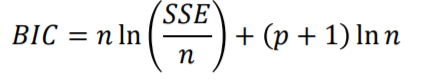
AIC는 n값이 로그이기 때문에 n값이 커질수록 점점 더 부정확한 값을 가지게 됩니다.
그렇기에 BIC는 단순히 p부분에 로그값을 붙여 줌으로써 이를 보정해준 값 입니다.
3. 회귀모델 검증
-
성능지표를 활용하여 회귀모델을 평가하는 것 또한 좋은 방법이나 회귀모델은 기본적인 가정하에 실시 되는 것 입니다.
- 모든 잔차는 랜덤하게 분포되어 있다.
- 이 때 잔차는 정규분포를 따른다.
-
그렇기 때문에 아래와 같은 시각화 자료를 이용하여 이를 검증합니다.
-
Residuals산점도
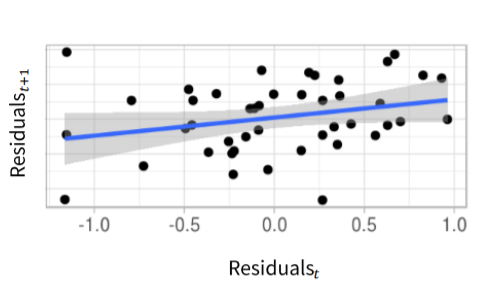
잔차는 랜덤해야 하기 때문에 t번째 잔차와 t+1번째 잔차가 선형상관관계를 가지지 않아야 합니다.
- normal Q-Q plot
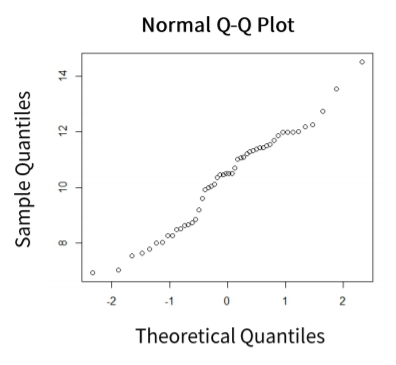
x축이 이론상 Y값, y축이 계산되어 얻어진 Y값, 즉 실제 Y와 $\hat Y$와의 관계가 선형에 가까워야 합니다.
이상적인 회귀모델은 Y와 $\hat Y$이 같기 때문에 Y=X 그래프를 그릴수록 좋은 모델입니다.
- Resuduals vs Fitted
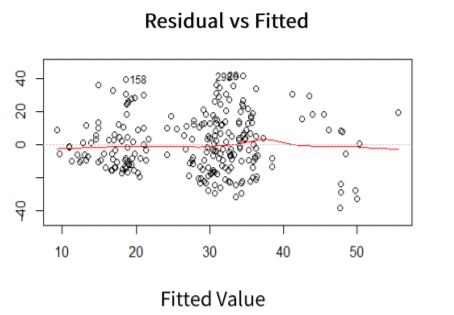
잔차는 랜덤해야하기 때문에 데이터의 갯수와 무관해야 합니다.
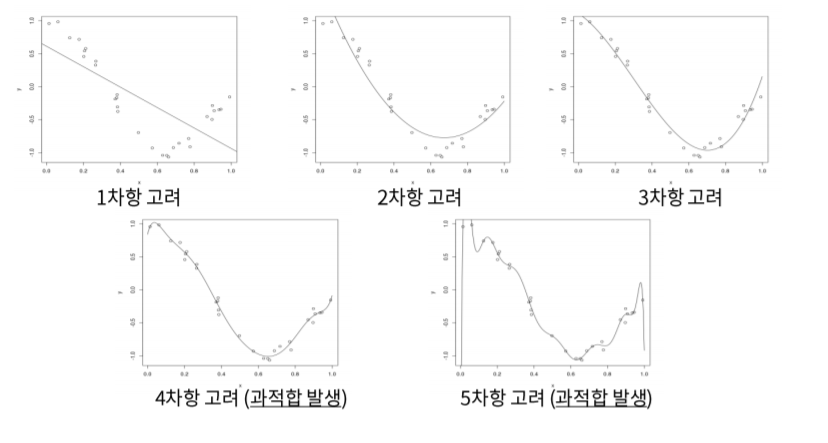
부록. 다항회귀분석
- **다항회귀분석(Polynomial regression)
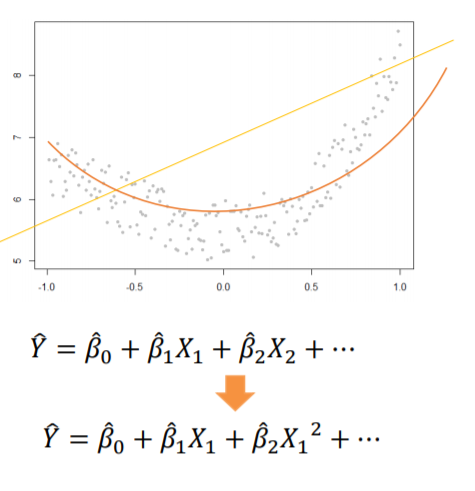
지금까지 선형회귀를 위해 단항식을 사용했다면 다항회귀분석은 곡선, 즉 다항식을 사용합니다.
비 선형을 사용하기에 항이 늘어난다는 점 이외에는 단항회귀분석, 선형회귀에 다른 점이 없습니다.
단 항이 늘어나 더 복잡한 곡선을 그릴수록 overfitting이 일어날 수 있습니다.
일반적으로 2차항, 혹은 3차항까지가 overfitting이 되지 않는다고 여겨지고 있습니다.
마치며
지금까지 선형회귀의 검정, 그리고 다항회귀 분석까지 알아보았습니다. 지금까지의 포스팅을 토대로 어느 데이터에 선형회귀 방식을 쓸지, 그리고 도출된 모델이 적합한지 평가하는데 도움이 되었으면 합니다.
