선형회귀 1
1. 단순 선형회귀 분석
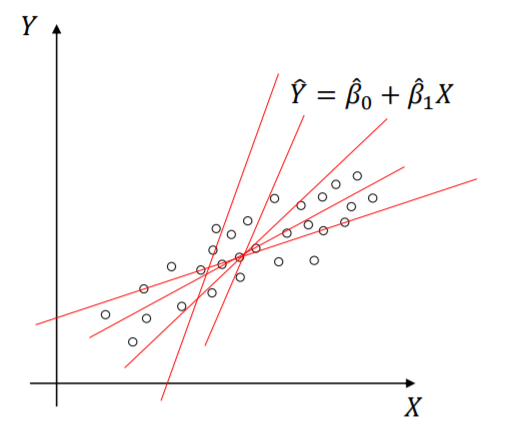
일차함수의 일반식인
y=ax+b와 비교하면 훨씬 쉽게 이해 할 수 있습니다.
이 중 데이터를 가장 잘 표현하는 직선은 직선과 데이터의 차이가 평균적으로 가장 작아지는 직선 입니다.
- 잔차(residual)

실제값과 우리가 추정한 값의 차이입니다.
선형회귀는 이러한 잔차를 최소화 하는 방향으로 추정합니다.
- SSE(Sum of Square Error)
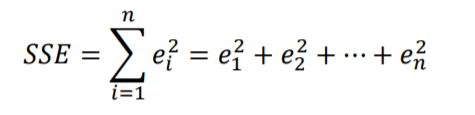
굳이 잔차를 제곱하는 이유는 음과 양의 값을 모두 가지는 잔차의 경우 합하였을때 0이 되는 경우가 한가지만 존재하지 않기 때문입니다.
절대값을 씌운다면 미분하여 최소값을 구할수 없기 때문에 제곱의 합을 사용합니다.
1.1 회귀 계수
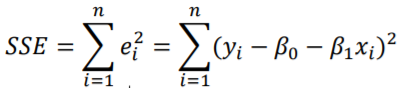

회귀 계수는 선형회귀 결과 나오는 함수의 기울기와 y절편 입니다.
SSE의 최솟값, 즉 미분하여 0이나오는 상황에서 구할 수 있으며 변수 위의 작대기는 ‘바’ 라고 읽으며 평균을 의미합니다.
1.2 선형회귀의 정확도 평가
- R squared
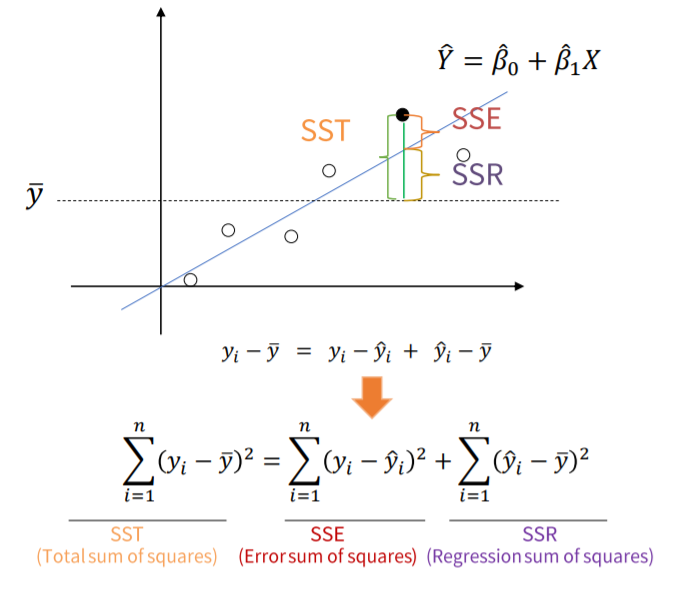
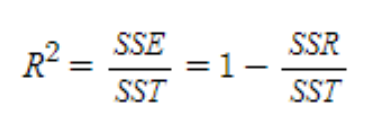
선형회귀의 정확도를 평가하기 위하여 R squared라는 수치를 사용합니다.
R squared는 0부터 1까지의 값을 가지며 예를들어 0.7이라는 수치가 나왔다면 모델의 설득력이 70%라는 것 입니다.
- R squared의 한계
회귀 분석은 잔차(residual)가 랜덤하게 분포되어 있다는 가정하에 계산하게 됩니다. 하지만 이러한 가정이 깨지게 된다면 잔차에 의존하는 R squared는 설득력을 잃게 됩니다.
의미가 없는 독립변수는 R squared의 값을 증가시킵니다.
1.3 회귀계수에 대한 검정
- 표준오차(SE)

회귀계수를 검정하기 위해 t분포를 이용하는데 여기에 계수의 표준오차를 구할 필요가 있습니다.
Sxx는 자유도를 의미합니다.
- 검정
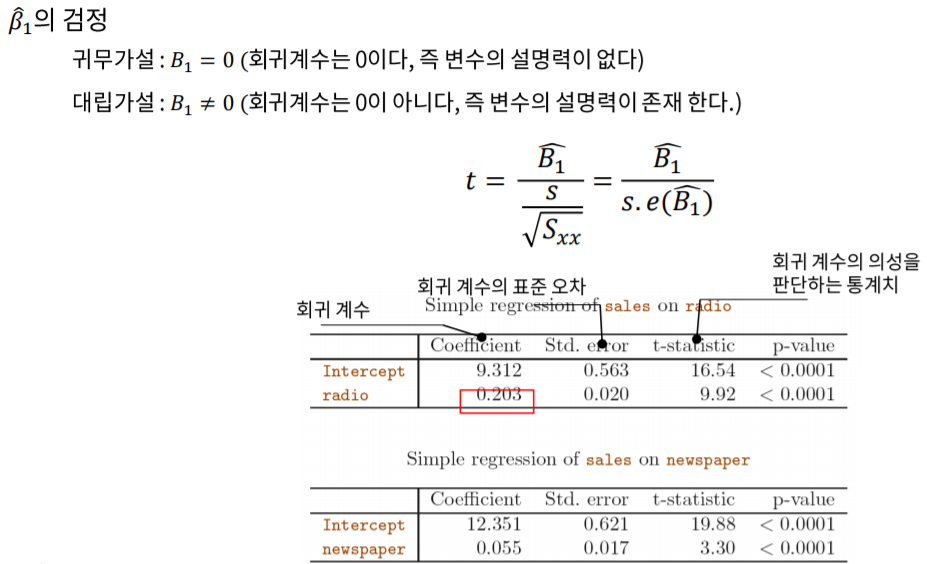
Intercept는 비교변수, 여기서는 매출입니다.
radio와 newspaper모두 회귀계수(B1), 표준오차(s.e(B1)), t 분포가 계산되며 t분포에 따른 p-value가 0.0001이하로 무척 작습니다.
p-value가 무척 작기 때문에 귀무가설은 채택되지 않으며 대립가설이 설득력을 얻습니다.
즉, radio와 newspaper는 결과값(Y)를 추정하는데 의미있는 변수라는 뜻 입니다.
2. 다중 선형회귀 분석
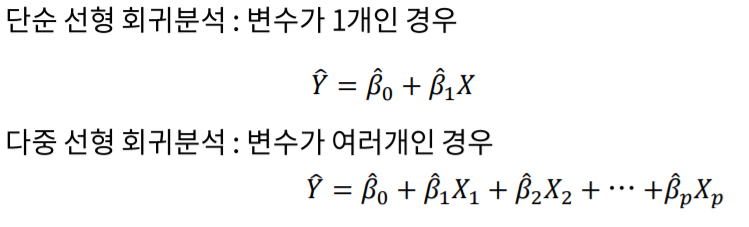
다중 선형회귀 분석은 단순 선형회귀와 크게 다르지 않습니다.
단순히 변수가 추가되고 그에 따른 계수가 추가되었을 뿐입니다.
각각의 회귀계수는 단순 선형회귀 때와 같이 각각의 변수에 따라 SSE를 편미분하여 0이 되는 값을 찾으면 됩니다.

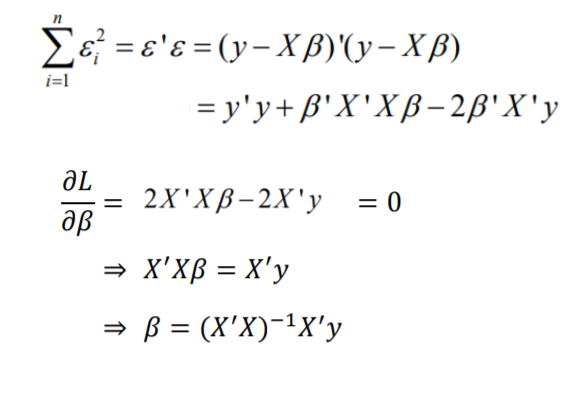
행렬로 표현한다면 위와 같이 표현할 수 있습니다.
또한 회귀계수 또한 SSE를 위와같이 미분하여 구할 수 있습니다. X’는 X의 transpose입니다.
다만 (X’X)의 역행렬을 구할 수 없을 경우 선형회귀 분석을 사용 할 수 없습니다.
2.1 다중 선형회귀 검정
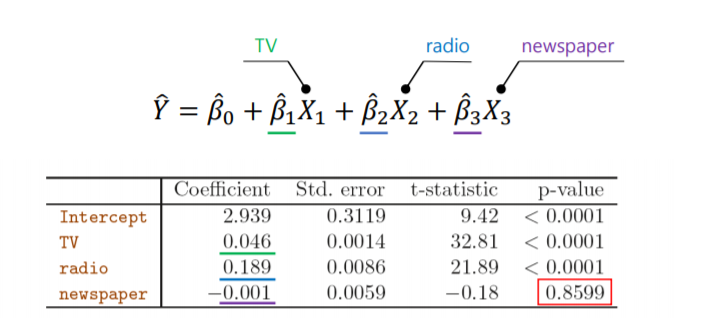
각각의 상수에 대하여 회귀계수가 0이라는 귀무가설을 세운 후 계산해 본 결과 입니다.
newspaper의 경우 p-value 가 상당히 높아 귀무가설을 채택, 즉 유의미한 영향을 미치지 못하였다고 판단합니다.
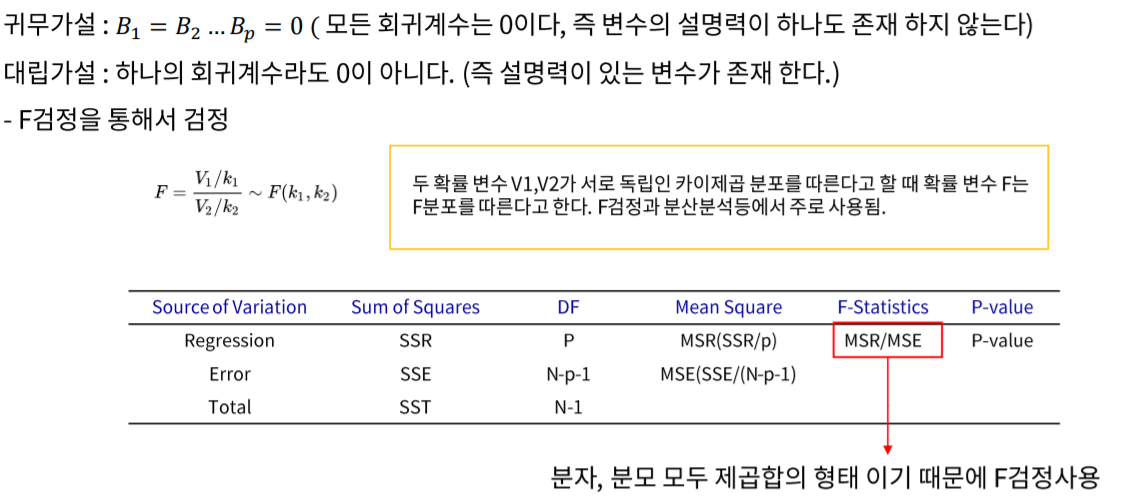
이번은 각각의 상수가 아닌 모든 상수가 전부 설득력을 가지지 않는다는 귀무가설을 세웠을 때 계산 방법입니다.
DF는 Degree of Freedom, 즉 자유도를 의미합니다.
변수는 추가되면 추가될 수록 기각하기 쉬워집니다. 이번 귀무 가설또한 기각하기 너무 쉬운 가설입니다.
F-statics를 결정짓는 변수 중 MSE 가 SSE/(n-p-1)인 반면 SSE는 제곱합이기 때문에 자유도, 즉 변수가 추가되면 추가될 수록 값이 커지게 되고 자연스럽게 F 값이 커져 기각하기 쉬워지는 것 입니다.
같은 이유로 R squared또한 상승합니다.
마치며
이번 포스팅은 선형회귀에 대해 알아보았습니다. 아직 선형회귀에 대한 내용이 더 있지만 우선 개념과 검정 그에 따른 수학적 계산을 위주로 포스팅 해 보았습니다.
