수학적 개념 2

1. 가능도 함수(Likelihood function)

• 확률분포함수(Probability Density Function)

전체 데이터, 즉 모수를 알고 있을 때 확률변수가 실현값을 예측하기 위한 분포함수입니다.

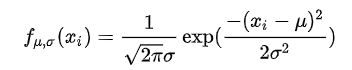
• 가능도함수(Likelihood function)

항상 전체 데이터, 모수를 알수 없기 때문에 표본을 사용합니다.

그렇기 때문에 이러한 표본을 통하여 모수의 평균값을 추정하기 위하여 사용하는 분포함수 입니다.

식으로는 확률분포함수와 동일하나 X가 아닌 평균을 변수로 인식합니다.

• MLE(Maximum Likelihood Estimator)

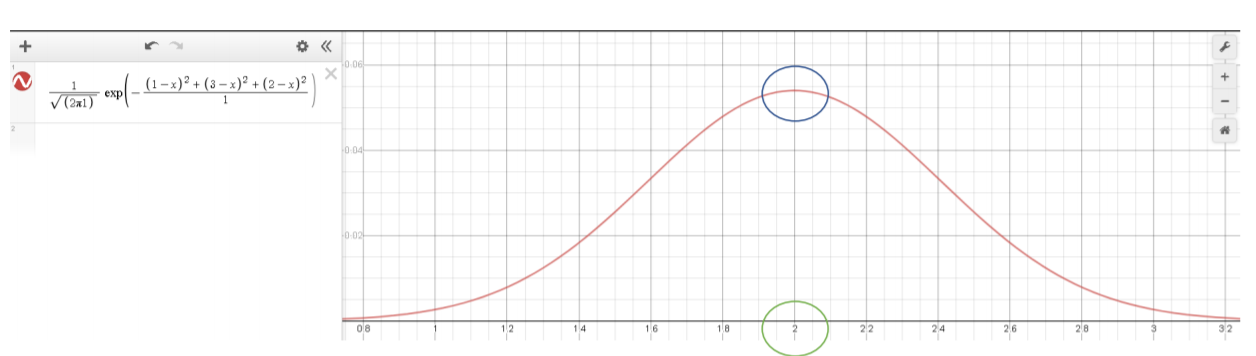
분포함수로 표현되는 가능도함수의 최댓값을 나타냅니다.

즉, 모수의 평균으로 추정될 확률이 가장 높은 값을 말합니다.

MLE를 구하는 방법은 가능도함수를 평균으로 미분하여 0이되는 평균값을 찾으면 됩니다.

2. 행렬의 미분

• 행렬의 계산에 있어 모든 vector는 coulmn vector라고 생각합니다.
• X가 row vector임을 표기하기 위해서는 X’(X의 transpose)라고 표기합니다.

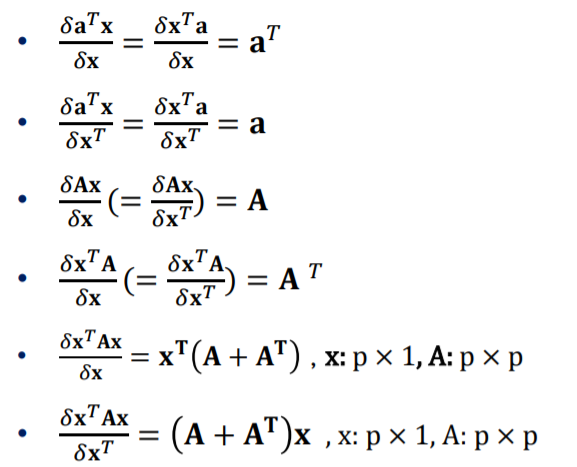
행렬의 미분결과는 일반 미분과 비슷한 결과를 가져옵니다.

다만 다른점이 있다면 행렬에는 차원이 존재하며 transpose된 변수로 미분을 하게 된다면 결과값 또한 transpose되서 나옵니다.

또한 마지막 두 공식은 AX^2을 미분한 것과 같은 것이며 x’Ax은(x’는 x의 transpose형) 행렬에선 차원이 맞지 않으면 서로 곱셈을 할 수 없기에 x^2이 존재 할 수 없기 때문에 위와 같은 형식이 된 것 입니다.

Symetric, 정방형일경우 A와 A’가 같기 때문에 2A라고 봐도 무방합니다.

마치며

이번 포스팅에서는 조금 생소한 수학적 개념을 따로 정리하여 포스팅 해 보았습니다. 행렬의 연산의 경우 다차원 연산을 하는 ML의 기본이 되는 연산이며 가능도 함수 또한 추정값을 보다 더 논리적으로, 정교하게 사용할 수 있게 도와줍니다.