수학적 개념 1
1. 통계
1.1 수치자료

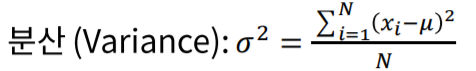

- 추정량(Estimator)
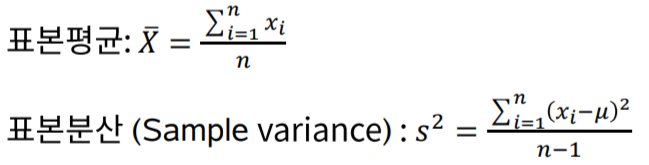
우리는 전체 집단을 측정 할 수 없기에 전체의 일부분, 즉 표본을 이용하여 전체 모수(Parameter)를 추정하게 됩니다.
이 때의 평균과 분산을 각각 위처럼 표시하고 정의합니다.
1.2 확률변수와 확률분포
- 확률변수 : 각각의 근원사건에 실수값을 대응하는 변수입니다.

- 확률분포 : 확률변수에서 확률값으로의 함수를 뜻합니다.
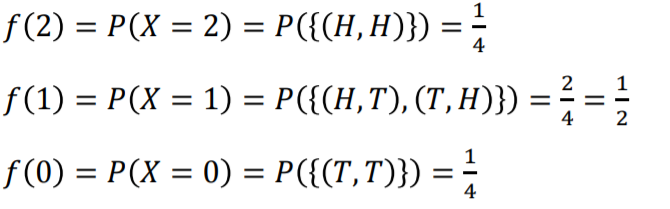
- 확률변수의 기댓값 : 확률변수의 중심 경향값입니다. 흔히 평균이라고 부릅니다.
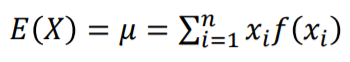
- 확률변수의 분산
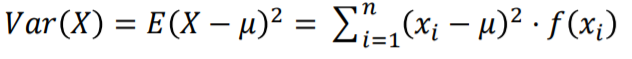
- 공분산
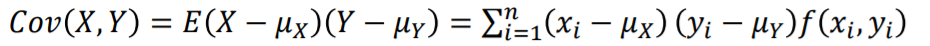
두개의 확률변수 X 와 Y 가 어떤 상호 관계를 가지는지에 대한 척도 입니다.
- 상관계수
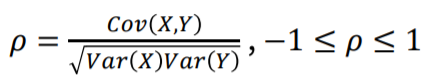
공분산은 X,Y의 크기에 따라 그 수치가 커지고 작아집니다.
이를 보정하기 위해 상관계수는 -1 부터 1 까지로 제한하여 어느정도의 상관관계를 가지는지 나타내는 척도 입니다.
1.3 통계적 추론
- 구간추정(Interver estimation)
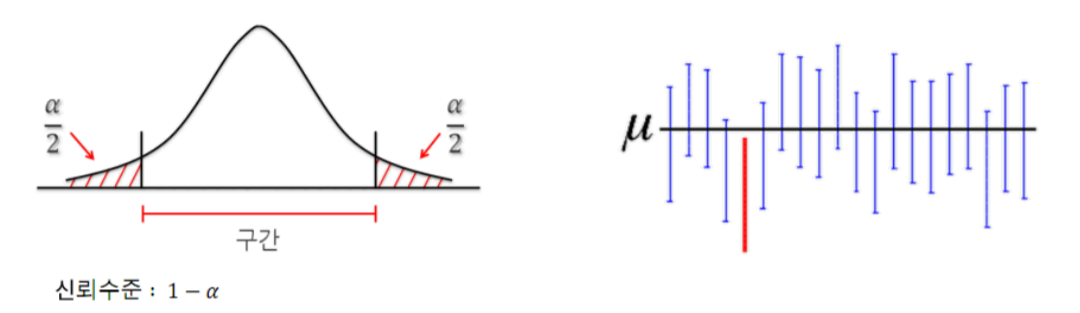
일정 신뢰구간 하에서 Parameter를 포함할 것으로 예상되는 구간을 제시합니다.
1.4 통계적 검정
- 대립가설(alternative hypothesis) H1
입증하여 주장하고자 하는 가설입니다.
- 귀무가설(null hypothesis) H0
대립가설을 증명하기 위하여 세우는 가설입니다.
이때 귀무가설 하에서 통계량의 분포를 아는 것이 검정의 핵심입니다.
이 때의 알파를 기각역이라 하며 신뢰구간에 따라 설정해 줄 수 있습니다.
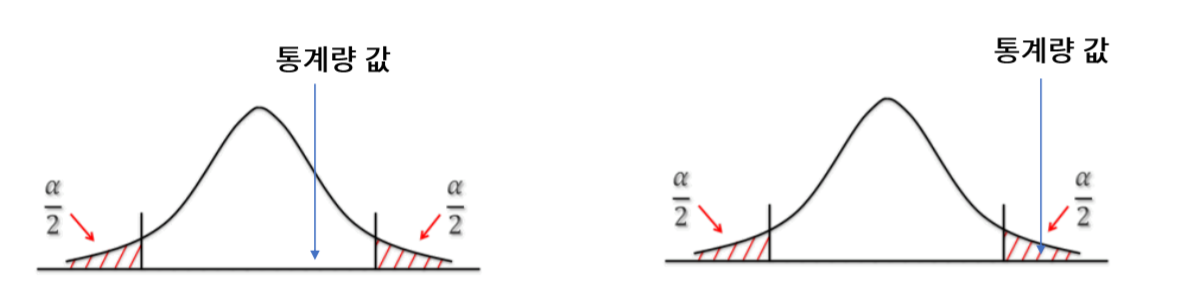
- 유의확률(p value)
주어진 검정 통계량값(X)을 기준으로 해당 값보다 대립가설을 더 선호하는 검정 통계량이 나올 확률 입니다.
즉 유의확률이 기각역을 기준으로 더 작다면 귀무가설(null hypothesis)를 기각합니다.
1.5 검정 통계량과 분포
- Z통계량
정규분포를 따르는 검정 통계량의 분포입니다.
즉 중심은 평균을 따르고 모양은 분산에 의해 결정됩니다.
n은 자유도(표본갯수 - 상수항을 포함한 변수 갯수)를 의미합니다.
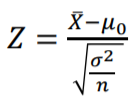
- t 분포
전체 집단의 분산값을 알 수 없으므로 표본분산 s를 사용한 분포입니다.
자유도, 즉 X에 영향을 미치는 요소(X1, X2, X3, … Xn)의 갯수에 따라 분포도의 모양이 달라지며 이 자유도가 커질수록 정규분포에 가까워집니다.
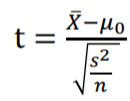
마치며
지금까지 ML을 위한 수학적 개념 중 통계에 대해 알아보았습니다. 이러한 통계적 지식은 ML을 통해 얻어진 추정치가 얼마만큼 신뢰할 수 있는지, 회귀계수를 통해 변수가 얼마나 설득력이 있는지 등을 계산하는데 사용됩니다. 추후에 ML 포스팅에서 이러한 수학적 개념을 참고하도록 하겠습니다.
